Geometric interpretation of the movements of the image point in the angle-domain

The geometric interpretation of the angle-domain transformation kinematics allows us to simplify equation (21) by showing that the terms multiplying the partial derivatives with respect to the angles are zero. Equation (21) simplifies to

$$\begin{eqnarray} \frac{\partial z_{\tilde{\gamma}}}{\partial \rho_{i}} = \frac{1... ..._r}{\partial S_r} \frac{\partial S_r}{\partial \rho_{i}} \right).\end{eqnarray}$$ (22)

Linearized perturbations caused by changes in L

Figure 5 graphically illustrates the image perturbation related to the first term in equation (22). It shows the movement of the image points (both in the subsurface-offset domain and the angle domain) caused by changes in the ray length L.

 

cig-2d-aniso-delta1-dipping-1 Figure 5 Linearized perturbations of the image-point locations caused by changes in the ray length L.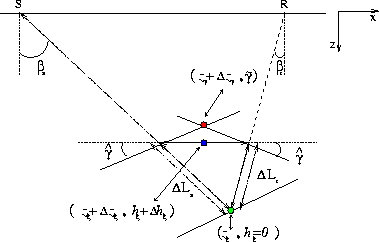

Linearized perturbations caused by changes in $\beta_s$

Figure 6 graphically illustrates the image perturbation related to the second term in equation (22). Perturbations in the angle $\beta_s$cause the subsurface offset-domain image to move along the tangent to the incident wavefront. Since this movement is constraint along the tangent, the image point in the angle-domain does not move no matter how large the corresponding movement in the subsurface offset domain is.

 

cig-2d-aniso-delta2-dipping-1 Figure 6 Linearized perturbations of the image-point locations caused by changes in 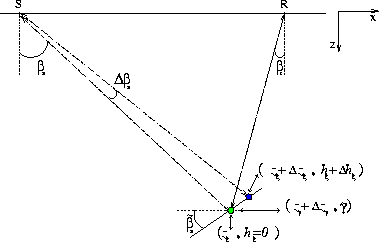$\beta_s$.

Linearized perturbations caused by changes in $\tilde{\beta}_s$

Figure 7 graphically illustrates the image perturbation related to the third term in equation (22). Since we linearize the depth of the image point around the correct migration velocity function, perturbations in the angle $\tilde{\beta}_s$ don't affect the depth of the imaging point (it is the main concept of ADCIGs).

 

cig-2d-aniso-delta3-dipping-1 Figure 7 Linearized perturbations of the image-point locations caused by changes in 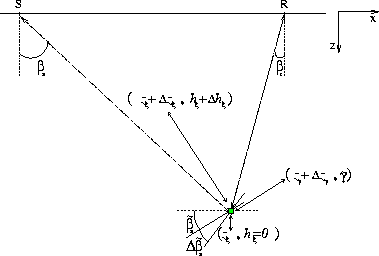$\tilde{\beta}_s$.