Next: Implementation of LSJIMP
Up: LSJIMP: Vyas and Brown
Previous: Introduction
LSJIMP models the recorded data as the superposition of primary reflections and
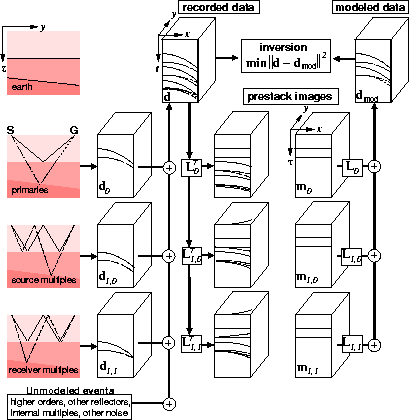
p orders of pegleg multiples from  multiple-generating surfaces. A schematic for LSJIMP is given in Figure
multiple-generating surfaces. A schematic for LSJIMP is given in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
An
.
An 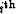 order pegleg splits into i+1 legs. If we denote the primaries
as
order pegleg splits into i+1 legs. If we denote the primaries
as 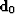 and the
and the 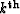 leg of the
leg of the 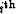 order pegleg from the
order pegleg from the
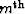 multiple generator as
multiple generator as 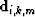 , the modeled data takes the
following form:
schem-LSJIMP-seg
, the modeled data takes the
following form:
schem-LSJIMP-seg
Figure 1 LSJIMP schematic. Assume that the recorded
data consist of primaries and pegleg multiples. Prestack imaging alone
(applying adjoint of modeling operator 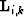 ) focuses signal events
in zero-offset traveltime (or depth) and offset (or reflection angle), but
leaves behind crosstalk events. If the
) focuses signal events
in zero-offset traveltime (or depth) and offset (or reflection angle), but
leaves behind crosstalk events. If the 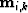 images contain only
signal, then we can model all the events in the data that we desire. The
LSJIMP inversion suppresses crosstalk and endeavors to fit the recorded data in
a least-squares sense. The model regularization operators used to suppress
crosstalk simultaneously enable LSJIMP to exploit the intrinsic redundancy
between and within the images to increase signal fidelity.
images contain only
signal, then we can model all the events in the data that we desire. The
LSJIMP inversion suppresses crosstalk and endeavors to fit the recorded data in
a least-squares sense. The model regularization operators used to suppress
crosstalk simultaneously enable LSJIMP to exploit the intrinsic redundancy
between and within the images to increase signal fidelity.

| 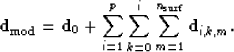 |
(1) |
If we have designed an imaging operator that produces primary and multiple images
with consistent signal (kinematics and angle-dependent amplitudes), then we
assume that we can model the important events in the data. We can rewrite equation
(1) as
| 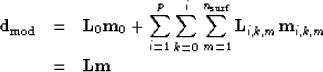 |
(2) |
| (3) |
where 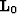 is the modeling operator of the primaries, and
is the modeling operator of the primaries, and 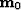 is the image of primaries. Similarly, for the
is the image of primaries. Similarly, for the 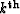 leg of the
leg of the
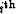 order pegleg from the
order pegleg from the 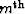 multiple generator,
multiple generator, 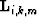 and
and 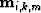 are modeling operator and image respectively.
are modeling operator and image respectively.
Brown (2004) derived appropriate imaging and amplitude correction operators to map the primary image, 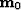 , into data-space primary events using the Normal Move-Out (NMO) operator,
, into data-space primary events using the Normal Move-Out (NMO) operator, 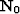 . Similarly, a given pegleg image,
. Similarly, a given pegleg image, 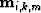 , is mapped into data space by sequentially applying the differential geometric spreading correction (
, is mapped into data space by sequentially applying the differential geometric spreading correction (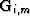 ), Snell resampling (
), Snell resampling (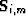 ), the Hetrogeneous-Earth Multiple NMO operator (HEMNO) (
), the Hetrogeneous-Earth Multiple NMO operator (HEMNO) (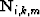 ), and finally, a reflection coefficient (
), and finally, a reflection coefficient (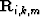 ). HEMNO is a slight improvement over NMO that takes into account kinematics of mildly dipping reflectors. Using these operators, we can rewrite equation (2) as follows:
). HEMNO is a slight improvement over NMO that takes into account kinematics of mildly dipping reflectors. Using these operators, we can rewrite equation (2) as follows:
| 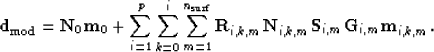 |
(4) |
The LSJIMP seeks to optimize the primary and multiple images, 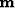 ,by minimizing the
,by minimizing the 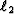 norm of the data residual, defined as the difference
between the recorded data,
norm of the data residual, defined as the difference
between the recorded data, 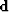 , and the modeled data,
, and the modeled data, 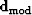 [equation (3)]:
[equation (3)]:
| 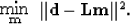 |
(5) |
Minimization (5) is under-determined for many choices of
prestack imaging operator, which implies an infinite number of
least-squares-optimal solutions. The problem of infinite optimal solutions manifests
itself as crosstalk leakage. Of this infinity of possible 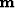 's, we seek the one which not only fits the
recorded data, but which also has minimum crosstalk leakage and maximum
consistency between signal events on different images. In general we compensate for a
correlated or poorly scaled data residual by adding a residual weighting
operator,
's, we seek the one which not only fits the
recorded data, but which also has minimum crosstalk leakage and maximum
consistency between signal events on different images. In general we compensate for a
correlated or poorly scaled data residual by adding a residual weighting
operator, 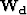 :
:
| ![\begin{displaymath}
\mbox{ \raisebox{-1.0ex}{ $\stackrel{\textstyle \mbox{min}}{...
...ert {\bf W_d} \left[ \bold d - \bold L \bold m \right] \Vert^2,\end{displaymath}](img28.gif) |
(6) |
where strictly speaking,
| ![\begin{displaymath}
\left( {\bf W_d}^T {\bf W_d} \right)^{-1} = {\rm cov}[\bold d].\end{displaymath}](img29.gif) |
(7) |
To effect the final step of LSJIMP and penalize crosstalk, we use three regularization operators. As discussed in detail by Brown (2004), the operators penalize roughness in reflection angle and between images, and also penalize the model after weighting with a prior model of the crosstalk on each 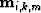 . For estimation of the optimal set of
. For estimation of the optimal set of 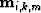 , we minimize a quadratic objective function which consists of the sum of the weighted
, we minimize a quadratic objective function which consists of the sum of the weighted 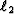 norms of the data residual [equation(6)] and of the three model residuals:
norms of the data residual [equation(6)] and of the three model residuals:
| ![\begin{displaymath}
\mbox{ \raisebox{-1.0ex}{ $\stackrel{\textstyle \mbox{min}}{...
...]} \Vert^2
\; + \; \epsilon_3^2 \Vert \bold r_m^{[3]} \Vert^2,\end{displaymath}](img30.gif) |
(8) |
where 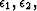 and
and 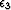 are scalars that balance the relative weight of the three model residuals (damping factors) with the data residual. These three residuals are calculated by differencing across images, differencing across offset, generating a crosstalk model, and calculating their penalty weights.
are scalars that balance the relative weight of the three model residuals (damping factors) with the data residual. These three residuals are calculated by differencing across images, differencing across offset, generating a crosstalk model, and calculating their penalty weights.





Next: Implementation of LSJIMP
Up: LSJIMP: Vyas and Brown
Previous: Introduction
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
An
.
An 
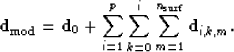
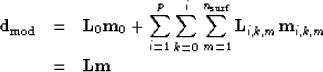
![]() , into data-space primary events using the Normal Move-Out (NMO) operator,
, into data-space primary events using the Normal Move-Out (NMO) operator, ![]() . Similarly, a given pegleg image,
. Similarly, a given pegleg image, ![]() , is mapped into data space by sequentially applying the differential geometric spreading correction (
, is mapped into data space by sequentially applying the differential geometric spreading correction (![]() ), Snell resampling (
), Snell resampling (![]() ), the Hetrogeneous-Earth Multiple NMO operator (HEMNO) (
), the Hetrogeneous-Earth Multiple NMO operator (HEMNO) (![]() ), and finally, a reflection coefficient (
), and finally, a reflection coefficient (![]() ). HEMNO is a slight improvement over NMO that takes into account kinematics of mildly dipping reflectors. Using these operators, we can rewrite equation (2) as follows:
). HEMNO is a slight improvement over NMO that takes into account kinematics of mildly dipping reflectors. Using these operators, we can rewrite equation (2) as follows: