




Next: Thomsen parameters
Up: ANISOTROPY DUE TO FRACTURES
Previous: ANISOTROPY DUE TO FRACTURES
Sayers and Kachanov (1991) also introduce a very interesting and
useful scheme
in the same paper that permits the calculation of constants for
anisotropic cracked media from estimates of the behavior (such as that
predicted by DS) for the isotropic case. This approach is a
tremendous simplification of an otherwise very difficult technical
problem. The key idea they use is to introduce an elastic potential
energy quadratic in the stress tensor that can be expressed in terms
of invariants of the stress tensor in various combinations involving the
``crack density tensor.'' This approach results in a fairly complicated energy
potential function involving nine distinct terms. But this function has the
advantage that, upon linearization in the crack density, it reduces to only
four terms. Two of these terms are the standard ones for the pure
(uncracked) medium and the remaining two terms contain the linear
contributions due to the cracks. Now it is not obvious that
linearization is permissible in the crack density ranges of interest,
but Sayers and Kachanov (1995) showed in later work that the
remaining contributions from the fourth rank crack-density tensor are
always small -- and therefore negligible in most situations of practical
interest. The neglect of these terms nevertheless implies a certain amount of
error in any calculation made based on their neglect, but -- if this
error is of the size of our measurement error or less -- it should not
be a serious impediment to studies and analysis of these systems.
To give one example, we find that the corrections to the compliance
matrix Sij due to the presence of an isotropic crack distribution
take the form:
| 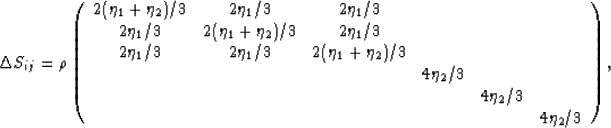 |
(1) |
where 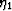 and
and 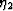 are the two coefficients appearing in the
Sayers and Kachanov (1991)
theory that depend on the presence of cracks, and
are the two coefficients appearing in the
Sayers and Kachanov (1991)
theory that depend on the presence of cracks, and 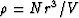 is the crack density (where N/V is the number desnity and r is
the radius of the flat cracks when they are penny-shaped as assumed here).
These two coefficients can be determined for any crack density
by computing the bulk and shear moduli from the compliance
matrix
is the crack density (where N/V is the number desnity and r is
the radius of the flat cracks when they are penny-shaped as assumed here).
These two coefficients can be determined for any crack density
by computing the bulk and shear moduli from the compliance
matrix 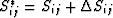 and comparing the results
one-to-one with the results from any effective medium theory one
trusts. For these purposes, the differential scheme (DS) is the one that
Sayers and Kachanov (1991) recommend, but I have shown elsewhere that
another scheme -- a symmetric self-consistent scheme that is
sometimes called the CPA (for coherent potential approximation) -
gives very comparable results. The results can also be compared to
rigorous bounds (this work is in progress)
and, therefore, also used to obtain rigorous upper bounds on
both
and comparing the results
one-to-one with the results from any effective medium theory one
trusts. For these purposes, the differential scheme (DS) is the one that
Sayers and Kachanov (1991) recommend, but I have shown elsewhere that
another scheme -- a symmetric self-consistent scheme that is
sometimes called the CPA (for coherent potential approximation) -
gives very comparable results. The results can also be compared to
rigorous bounds (this work is in progress)
and, therefore, also used to obtain rigorous upper bounds on
both 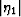 and
and 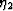 . I have done some initial studies of
this type and found that the value of
. I have done some initial studies of
this type and found that the value of 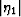 is generally much smaller in magnitude that of
is generally much smaller in magnitude that of 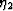 .In particular,
.In particular, 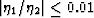 is typical of the observed results for both DS and CPA.
is typical of the observed results for both DS and CPA.
The real advantage of this approach can now be shown very simply
using a couple of examples.
First, consider the situation in which all the cracks in the system
have the same vertical (z-)axis of symmetry. Then, the cracked/fractured
system is not isotropic, and we have the compliance correction matrix
| 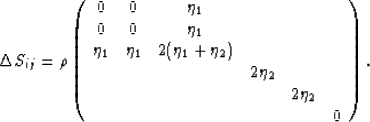 |
(2) |
Now it is also not difficult to see that, if the cracks were oriented
instead so that all their normals were pointed horizontally along the
x-axis, then I would have one permutation of this matrix and, if
instead they were all pointed horizontally along the y-axis, then I would
have a third permutation of the matrix. If I then want to understand
the isotropic correction matrix in (1), I can average
these three permutations: just add the three  's together
and then divide by three. Having done that, I exactly recover
the isotropic compliance corrections matrix displayed in (1).
This construction shows in part both the power and the simplicity of
the Sayers and Kachanov (1991) approach.
's together
and then divide by three. Having done that, I exactly recover
the isotropic compliance corrections matrix displayed in (1).
This construction shows in part both the power and the simplicity of
the Sayers and Kachanov (1991) approach.

Next, consider the case when all cracks have their normals lying
randomly in parallel planes. Then, if the parallel planes are taken to
be horizontal, the cracks are all vertically aligned as in Figure 1.
So, I immediately find the anisotropic (i.e., vertical
transverse isotropy or VTI) result that
| 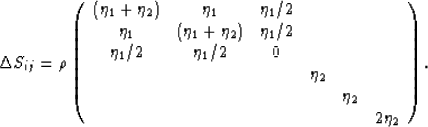 |
(3) |
The reader should check that adding two-thirds of (3)
to one-third of (2) recovers (1),
since this combination also represents an isotropic ensemble of fractures.
This same basic concept then works very well for any assumed symmetry
that we might like to model. There is no additional work to be done
once (i) the isotropic results are known (for some EMT)
and (ii) the layout of the two  's
in the correction matrix
's
in the correction matrix 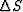 have been determined once and for
all for a given elastic symmetry resulting from a specific choice of
crack orientation distribution. Sayers and Kachanov (1991) give a
precise prescription for this. Although I make use of this
prescription here,
I will not show the details in order to avoid some of the
mathematical complications inherent in their tensorial expressions.
have been determined once and for
all for a given elastic symmetry resulting from a specific choice of
crack orientation distribution. Sayers and Kachanov (1991) give a
precise prescription for this. Although I make use of this
prescription here,
I will not show the details in order to avoid some of the
mathematical complications inherent in their tensorial expressions.
There are interesting and important questions of uniqueness related to
the inverse problem (i.e., deducing the  's from seismic
wave observations) since more than one type of distribution can give
rise, for example, to vertical transverse isotropy (VTI). Then, the
question is whether quantities such as the Thomsen parameters of anisotropy
can help us to remove some of these possible ambiguities from the
interpretations of field measurements.
's from seismic
wave observations) since more than one type of distribution can give
rise, for example, to vertical transverse isotropy (VTI). Then, the
question is whether quantities such as the Thomsen parameters of anisotropy
can help us to remove some of these possible ambiguities from the
interpretations of field measurements.





Next: Thomsen parameters
Up: ANISOTROPY DUE TO FRACTURES
Previous: ANISOTROPY DUE TO FRACTURES
Stanford Exploration Project
4/5/2006
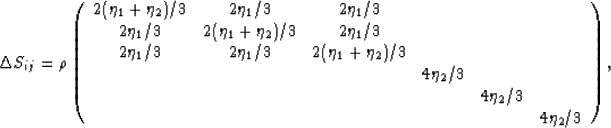
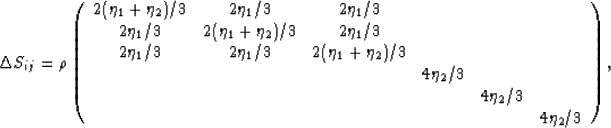
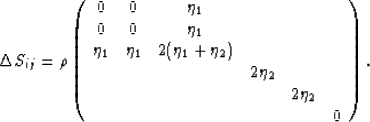
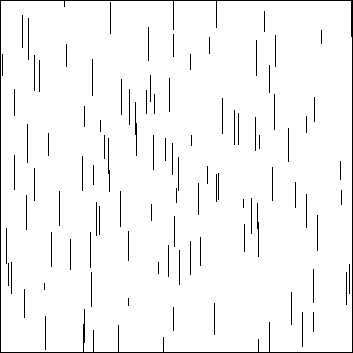
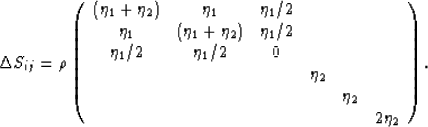
![]() 's
in the correction matrix
's
in the correction matrix ![]() have been determined once and for
all for a given elastic symmetry resulting from a specific choice of
crack orientation distribution. Sayers and Kachanov (1991) give a
precise prescription for this. Although I make use of this
prescription here,
I will not show the details in order to avoid some of the
mathematical complications inherent in their tensorial expressions.
have been determined once and for
all for a given elastic symmetry resulting from a specific choice of
crack orientation distribution. Sayers and Kachanov (1991) give a
precise prescription for this. Although I make use of this
prescription here,
I will not show the details in order to avoid some of the
mathematical complications inherent in their tensorial expressions.
![]() 's from seismic
wave observations) since more than one type of distribution can give
rise, for example, to vertical transverse isotropy (VTI). Then, the
question is whether quantities such as the Thomsen parameters of anisotropy
can help us to remove some of these possible ambiguities from the
interpretations of field measurements.
's from seismic
wave observations) since more than one type of distribution can give
rise, for example, to vertical transverse isotropy (VTI). Then, the
question is whether quantities such as the Thomsen parameters of anisotropy
can help us to remove some of these possible ambiguities from the
interpretations of field measurements.