




Next: Regularization through Monitor Functions
Up: Theoretical Overview
Previous: Theoretical Overview
Generalized Laplacian systems can be solved by many different ways;
however, numerical solution often is facilitated through intermediate
mappings to meshes exhibiting many attributes of the final grid. This
consists of a composite of a transformation - 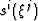 - from a
Cartesian
- from a
Cartesian 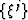 to an intermediate basis
to an intermediate basis 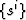 , and a
transformation - xk(sj) - from
, and a
transformation - xk(sj) - from 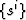 to the final
coordinate mesh
to the final
coordinate mesh 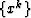 . Notationally, the composite mapping
transforms for the N-D problem are,
. Notationally, the composite mapping
transforms for the N-D problem are,
| 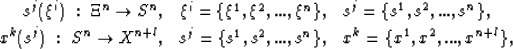 |
|
| (2) |
Note that coordinate system 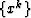 may be of a greater dimension
than
may be of a greater dimension
than 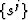 , which allows for composite mapping operations of
, which allows for composite mapping operations of
![$x^k \left[s^j \left(\xi^i \right)\right]\; : \; \Xi^n \rightarrow X^{n+k}$](img17.gif) that
project a 2-D surface into 3-D space (see figure
that
project a 2-D surface into 3-D space (see figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for
an example).
Example
for
an example).
Example
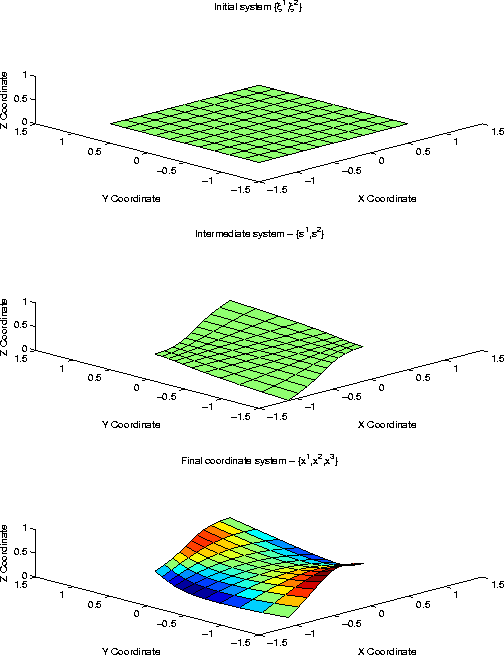
Figure 1 Meshing example for mapping a 2-D
Cartesian domain to a surface in a 3-D volume. Top panel: Regular
Cartesian mesh 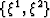 ; Middle panel: Intermediate
transformation domain
; Middle panel: Intermediate
transformation domain 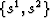 ; and Bottom panel: Surface in
middle panel projected onto 3-D surface
; and Bottom panel: Surface in
middle panel projected onto 3-D surface 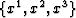 where
increasing grey scale intensity represents increasing height.
where
increasing grey scale intensity represents increasing height.

Coordinate system transformations - 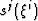 and xk(sj) - are
described in differential geometry through metric tensor, gij,
which relates the geometry of a coordinate system
and xk(sj) - are
described in differential geometry through metric tensor, gij,
which relates the geometry of a coordinate system 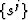 to that of
to that of
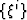 Guggenheimer (1977). The metric tensor is symmetric
(i.e. gij=gji) and has elements given by,
Guggenheimer (1977). The metric tensor is symmetric
(i.e. gij=gji) and has elements given by,
| 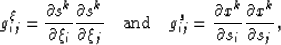 |
(3) |
where the metric tensor superscript specifies the coordinate system in
which the operator is defined. (Note that summation notation -
gii = g11+g22+g33 - is implicit for any repeated
indicies found in the paper.) The associated metric tensor gij
is related to the metric tensor through gij = gij/|gs| where
gs is the metric tensor determinant. Through use of this
differential geometric framework, the governing set of differential
gridding equations Liseikin (2004) become,
| ![\begin{eqnarray}
D^{\xi}[s^j] = \frac{1}{\sqrt{g_s} } \,\frac{\partial}{\partial...
...t\vert _{\partial S^n}
= \phi^i \left[ s^j \right], \quad i,j=1,n.\end{eqnarray}](img23.gif) |
(4) |
| (5) |
Equations 4 represent the N generalized Laplace's
equations acting on coordinate fields 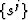 , and
equations 5 map the boundary values of each coordinate
field
, and
equations 5 map the boundary values of each coordinate
field ![$\phi^i \left[s^j \right]$](img24.gif) to the boundary of domain
to the boundary of domain  . As
posed, equations 4 and 5 provide no
guarantee that generated grids will exhibit appropriate
characteristics because no mesh regularization has yet been enforced.
. As
posed, equations 4 and 5 provide no
guarantee that generated grids will exhibit appropriate
characteristics because no mesh regularization has yet been enforced.





Next: Regularization through Monitor Functions
Up: Theoretical Overview
Previous: Theoretical Overview
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for
an example).
for
an example).
![]() and xk(sj) - are
described in differential geometry through metric tensor, gij,
which relates the geometry of a coordinate system
and xk(sj) - are
described in differential geometry through metric tensor, gij,
which relates the geometry of a coordinate system ![]() to that of
to that of
![]() Guggenheimer (1977). The metric tensor is symmetric
(i.e. gij=gji) and has elements given by,
Guggenheimer (1977). The metric tensor is symmetric
(i.e. gij=gji) and has elements given by,
![\begin{eqnarray}
D^{\xi}[s^j] = \frac{1}{\sqrt{g_s} } \,\frac{\partial}{\partial...
...t\vert _{\partial S^n}
= \phi^i \left[ s^j \right], \quad i,j=1,n.\end{eqnarray}](img23.gif)