Introduction

Anisotropy is becoming increasingly important in seismic imaging. If anisotropy is not included in migration, reflectors will not be imaged at the right positions, or even worse, they will be defocused. However, imaging in a general anisotropic medium is still a challenging problem. A vertical transversely isotropic (VTI) medium is one of the simplest and most practical approximations for anisotropic media in seismic imaging. Compared to that of isotropic media, the dispersion relation of VTI media is much more complicated. As a result, phase-shift-based methods Ferguson and Margrave (1998); Rousseau (1997) and explicit convolution methods Baumstein and Anderson (2003); Ren et al. (2005); Shan and Biondi (2005); Uzcategui (1995); Zhang et al. (2001a,b) are usually used in anisotropic migration, because the complex dispersion relation does not increase the difficulty of these algorithms. However, phase shift with interpolation requires a lot of reference wavefields, because there are two Thomsen anisotropy parameters in addition to the vertical velocity. Explicit convolution methods do not guarantee stability, and they also require long convolution filters to achieve good accuracy.

The implicit finite-difference method has been one of the most attractive migration methods for isotropic media. It can handle lateral variation naturally and guarantee stability. Traditional finite-difference methods, such as the 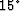$15^\circ$ equation Claerbout (1971) and the 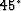$45^\circ$ equation Claerbout (1985), approximate the dispersion relation by the truncation of Taylor series. Lee and Suh (1985) approximate the square-root equation with rational functions, and optimize the coefficient with least-squares. This can achieve a scheme accurate to 65^o. It is much more difficult to design an implicit finite-difference method for VTI media, because of the complicated dispersion relation. Under the weak anisotropy assumption, Ristow and Ruhl (1997) design an implicit scheme for VTI media. Liu et al. (2005) apply a phase-correction operator Li (1991) after the finite-difference operator for VTI media and improve the accuracy.

In this paper, I present an optimized one-way wave equation for VTI media and introduce a table-driven, implicit finite-difference method for laterally varying media. I also apply the phase-correction filter to reduce the error. I test the scheme with synthetic and real data.