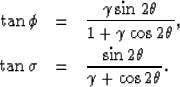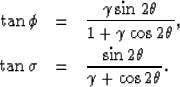Transformation into independent angles

Following definition 3, and after explicitly computing the full-aperture angle with equation 4, we have almost all the tools to explicitly separate the full-aperture angle into its two components, the P-incidence angle (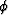$\phi$), and the S-reflection angle ($\sigma$). Snell's law, and the P-to-S velocity ratio are the final components for this procedure. After basic algebraic and trigonometric manipulations, the final expressions for both of the independent angles are

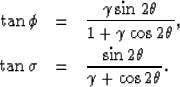$$\begin{eqnarray} \tan{\phi} &=& \frac{\gamma \sin{2\theta}}{1+\gamma \cos{2\thet... ...r\\ \tan{\sigma} &=& \frac{\sin{2\theta}}{\gamma + \cos{2\theta}}.\end{eqnarray}$$ (5)

This is clearly a non-linear relation among the angles. The main purpose of this set of equations is to observe and analyze the kinematics of the P-incidence wave, and the S-reflected wave. This analysis might lead to estimates of independent velocity perturbations for both the P-velocity model and the S-velocity model. The following section describes the proposed methodology to implement both equation 4 and system 5