




Next: REFERENCES
Up: Artman: Inversion shortcuts
Previous: Passive data
Inversion schemes for various Radon transforms
Artman and Guitton (2005); Artman and Sacchi (2003); Guitton (2004), have been proposed
to provide sparse model spaces for data analysis and noise removal.
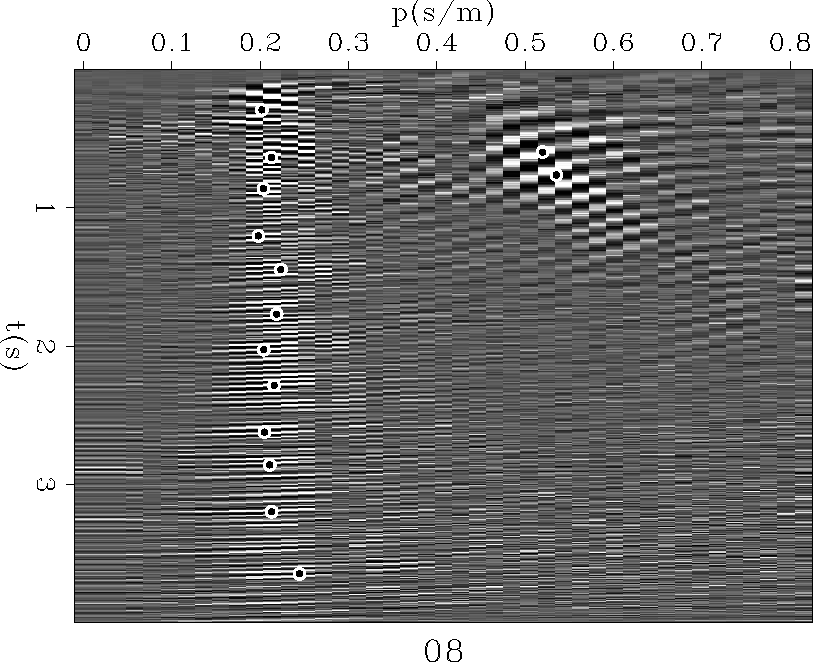
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of 20 iterations of hyperbolic Radon
transform performed on gather 08 from the Yilmaz data collection. Coordinates
selected by LA are overlain. I purposefully parameterized the model
space to include slowness values twice those necessary. The picks
remain stable with or without including this aphysical part of the
model domain. With a threshold of 1% of the maximum value in the
model space, the modified algorithm considered only 500 out of 43,000
coordinates for potential selection. The algorithm started with 200 evenly
distributed coordinate pairs and returned with 14 optimally
representative coordinates.
shows the result of 20 iterations of hyperbolic Radon
transform performed on gather 08 from the Yilmaz data collection. Coordinates
selected by LA are overlain. I purposefully parameterized the model
space to include slowness values twice those necessary. The picks
remain stable with or without including this aphysical part of the
model domain. With a threshold of 1% of the maximum value in the
model space, the modified algorithm considered only 500 out of 43,000
coordinates for potential selection. The algorithm started with 200 evenly
distributed coordinate pairs and returned with 14 optimally
representative coordinates.
shot
Figure 7 Hyperbolic Radon transform model
domain of shot 08 from the Yilmaz data collection. 20 iterations of
least-squares inversion were performed. 14 coordinates selected by
LA are overlain. Without inclusion of the inappropriate high
slowness values on the right side of the plot, the remaining picks
remain stable.
|
|  |





I introduce Lloyd's algorithm as a tool to optimally represent the
statistics of the model space from incomplete inversions. The
modified algorithm selects coordinates with high amplitude surrounded
by substantial energy. Thus isolated, powerful outliers are
neglected. By optimally parsing potentially large multi-dimensional
model spaces, the algorithm can cut short costly inversion iterations
and focus an interpreter's attention to important locations within
potentially large model domains. The algorithm returns stable
solutions even in the presence of substantial noise.
The algorithm is very simple, easy to modify, has few parameters, and
very fast. Using the algorithm depends on parameters being
correlable. For multidimensional cases, uncorrelated parameters
can simply be concatenated to an existing axis. Thus hypercubes of
correlable and uncorrelable parameters can be evaluated
simultaneously.
The next step in evaluating the effectiveness of using the algorithm
to select optimal parameters would be to migrate data with a velocity
model derived from RMS velocities selected by LA. This could
potentially dovetail with the velocity uncertainty analysis presented
in ().
Planewave decomposition of passive data to characterize non-obvious
sources does not work. Until traces have been correlated, analysis
transforms will simply redistribute the random character of the raw
data. Unfortunately, correlating the wavefield destroys all the
unique character of individual sources including timing, waveform,
location and much of the spectral content information.
Thanks to Bob Clapp for the introduction of LA to the group and good
discussions with Jeff Shragge on potential uses.





Next: REFERENCES
Up: Artman: Inversion shortcuts
Previous: Passive data
Stanford Exploration Project
4/5/2006

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of 20 iterations of hyperbolic Radon
transform performed on gather 08 from the Yilmaz data collection. Coordinates
selected by LA are overlain. I purposefully parameterized the model
space to include slowness values twice those necessary. The picks
remain stable with or without including this aphysical part of the
model domain. With a threshold of 1% of the maximum value in the
model space, the modified algorithm considered only 500 out of 43,000
coordinates for potential selection. The algorithm started with 200 evenly
distributed coordinate pairs and returned with 14 optimally
representative coordinates.
shows the result of 20 iterations of hyperbolic Radon
transform performed on gather 08 from the Yilmaz data collection. Coordinates
selected by LA are overlain. I purposefully parameterized the model
space to include slowness values twice those necessary. The picks
remain stable with or without including this aphysical part of the
model domain. With a threshold of 1% of the maximum value in the
model space, the modified algorithm considered only 500 out of 43,000
coordinates for potential selection. The algorithm started with 200 evenly
distributed coordinate pairs and returned with 14 optimally
representative coordinates.