




Next: Interpolation with non-stationary PEFs
Up: Curry: Interpolation with pseudo-primariesPseudo-primary
Previous: INTRODUCTION
Pseudo-primaries can be generated by computing Shan and Guitton (2004)
| 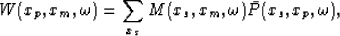 |
(1) |
where W is the pseudo-primary data, 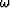 is frequency, xs
is the shot location, xp is the surface location,
is frequency, xs
is the shot location, xp is the surface location, 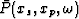 is the complex
conjugate of the original trace at (xs,xp) and M are the multiple
reflections recorded at xm. In this equation, the cross-correlation of
the first-order multiples in M with the primaries and first-order
multiples in P produces primaries and zero-lag components, respectively.
Cross-correlation of the second-order multiples in M with the
primaries, first-order, and second-order multiple reflections in P
produces first-order multiples, primaries, and zero-lag components,
respectively. With higher orders of multiples this trend continues.
is the complex
conjugate of the original trace at (xs,xp) and M are the multiple
reflections recorded at xm. In this equation, the cross-correlation of
the first-order multiples in M with the primaries and first-order
multiples in P produces primaries and zero-lag components, respectively.
Cross-correlation of the second-order multiples in M with the
primaries, first-order, and second-order multiple reflections in P
produces first-order multiples, primaries, and zero-lag components,
respectively. With higher orders of multiples this trend continues.
Pseudo-primaries generated in this fashion contain subsurface
information that would not be recorded with a non-zero minimum offset.
One example of this is a first-order multiple that reflects at the free
surface within the recording array, resulting in near offsets being
recorded when that wave returns to the surface. An example of this is
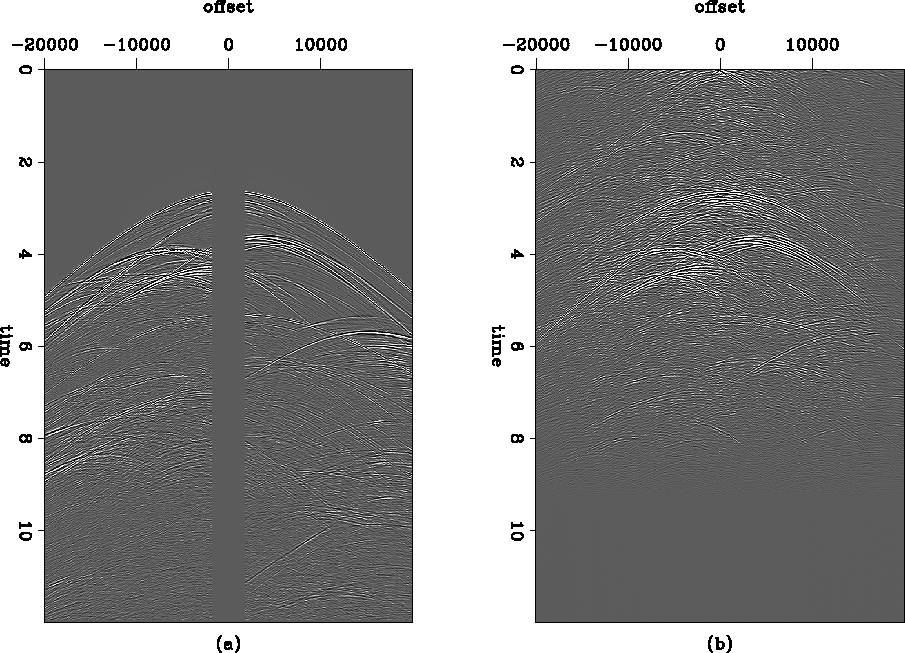
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , where (a) is a single Sigsbee2B shot (including the negative offsets
predicted by reciprocity) but with offsets less than 2000 feet
removed, and (b) is the corresponding pseudo-primaries for the same
area, which is generated in part with (a).
, where (a) is a single Sigsbee2B shot (including the negative offsets
predicted by reciprocity) but with offsets less than 2000 feet
removed, and (b) is the corresponding pseudo-primaries for the same
area, which is generated in part with (a).
shot
Figure 1 (a) Original
shot record and (b) pseudo-primaries for the same area from the
Sigsbee2B dataset.





We can see in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) where the first
and second-order multiples in P map to in the zero-lag at the top of the
image. We can also see a lot of near-offset information present in the
pseudo-primaries that is not present in the recorded primaries.
However, simply replacing the missing near offsets of the primaries with
the corresponding pseudo-primaries would not yield a satisfactory result
due to the crosstalk and noise in the pseudo-primary shot.
where the first
and second-order multiples in P map to in the zero-lag at the top of the
image. We can also see a lot of near-offset information present in the
pseudo-primaries that is not present in the recorded primaries.
However, simply replacing the missing near offsets of the primaries with
the corresponding pseudo-primaries would not yield a satisfactory result
due to the crosstalk and noise in the pseudo-primary shot.





Next: Interpolation with non-stationary PEFs
Up: Curry: Interpolation with pseudo-primariesPseudo-primary
Previous: INTRODUCTION
Stanford Exploration Project
4/5/2006
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , where (a) is a single Sigsbee2B shot (including the negative offsets
predicted by reciprocity) but with offsets less than 2000 feet
removed, and (b) is the corresponding pseudo-primaries for the same
area, which is generated in part with (a).
, where (a) is a single Sigsbee2B shot (including the negative offsets
predicted by reciprocity) but with offsets less than 2000 feet
removed, and (b) is the corresponding pseudo-primaries for the same
area, which is generated in part with (a).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) where the first
and second-order multiples in P map to in the zero-lag at the top of the
image. We can also see a lot of near-offset information present in the
pseudo-primaries that is not present in the recorded primaries.
However, simply replacing the missing near offsets of the primaries with
the corresponding pseudo-primaries would not yield a satisfactory result
due to the crosstalk and noise in the pseudo-primary shot.
where the first
and second-order multiples in P map to in the zero-lag at the top of the
image. We can also see a lot of near-offset information present in the
pseudo-primaries that is not present in the recorded primaries.
However, simply replacing the missing near offsets of the primaries with
the corresponding pseudo-primaries would not yield a satisfactory result
due to the crosstalk and noise in the pseudo-primary shot.