Non-technical technique overview

This section briefly describes the wave-equation migration from topography (TopoWEM) approach presented in Shragge and Sava (2004). Two theoretical developments are central to the technique: i) generating an orthogonal grid conformal with the acquisition surface using a conformal mapping approach; and ii) adapting wave-propagation physics to be consistent with the geometry of the computational mesh using Riemannian wavefield extrapolation (RWE) Sava and Fomel (2005). Conformal mapping transforms can be manipulated to generate an orthogonal coordinate system by computing a mapping from a topographically influenced domain to a rectangular mesh (c.f. Figure ). First, the image of the boundary points in the physical domain (upper left) is found in the canonical domain (upper right) through composite mapping $g\cdot f^{-1}$ (where g and f^-1 represent mappings from the physical domain to the unit circle and from the unit circle to a rectangle, respectively). A uniform mesh, specified in the canonical domain (lower right), is then mapped to the physical domain (bottom left) using the inverse relation $g^{-1} \cdot f$, creating an orthogonal mesh conformal to the topographic surface.

 

map1 Figure 1 Cartoon showing the conformal mapping transform between topographic and rectangular domains. Top left: topographic domain with data acquisition points; Top right: domain boundary in top left mapped to a rectangular domain under mapping 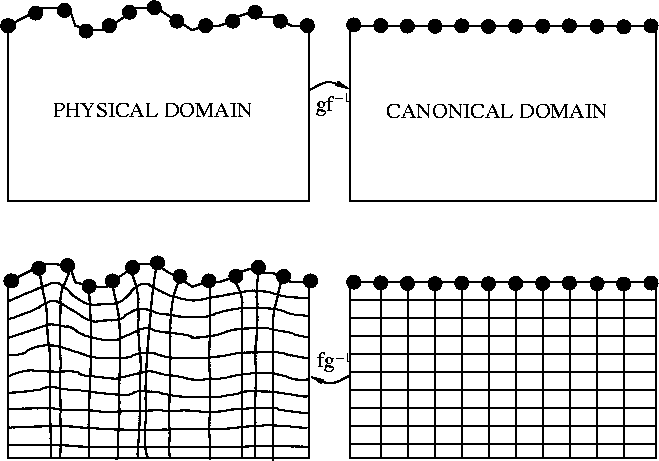$g\cdot f^{-1}$; Bottom right: uniform grid in canonical domain; and bottom left: (locally) orthogonal grid in physical domain generated by mapping grid in bottom right under relation $g^{-1} \cdot f$.

The second step is to specify the RWE extrapolation equations appropriate for the generated topographic coordinate system. This approach specifies a wave-equation dispersion appropriate for one-way wavefield extrapolation in generalized coordinate systems. Shragge and Sava (2004) discusses how to perform wave-equation migration directly from topographic coordinate systems, and illustrates this approach with a synthetic 2D data example.