|
mul_sktch7
Figure 18 Sketch illustrating that diffracted multiples may map to positive subsurface offsets. | 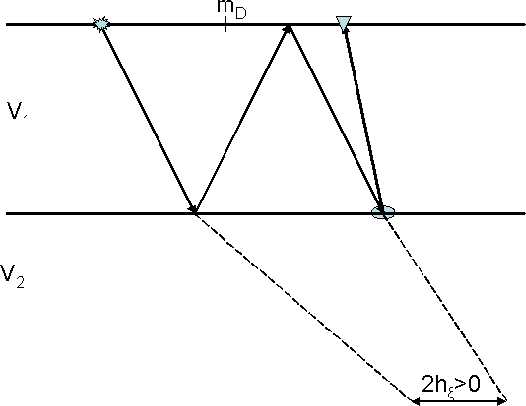 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . We can still separate
these multiples from the primaries, but that requires the application of an
appropriate Radon transform. An apex-shifted tangent-squared Radon transform
was applied by Alvarez et. al. 2004 to a real 2D section
with good results, but the basic assumption there was that of no ray-bending
at the water-bottom interface. It is expected that the more accurate
equations derived here will allow the design of a better Radon transform and
therefore a better degree of separation between primaries and diffracted
multiples. This is the subject of continuing research.
. We can still separate
these multiples from the primaries, but that requires the application of an
appropriate Radon transform. An apex-shifted tangent-squared Radon transform
was applied by Alvarez et. al. 2004 to a real 2D section
with good results, but the basic assumption there was that of no ray-bending
at the water-bottom interface. It is expected that the more accurate
equations derived here will allow the design of a better Radon transform and
therefore a better degree of separation between primaries and diffracted
multiples. This is the subject of continuing research.
|
mul_sktch7
Figure 18 Sketch illustrating that diffracted multiples may map to positive subsurface offsets. |  |
For the non-diffracted multiple from a flat water-bottom the mapping between
the image-space coordinates and the data-space coordinates is essentially
2D since ![]() , which allowed the computation of closed-form expressions
for the residual moveout of the multiples in both SODCIGs and ADCIGs. For
diffracted multiples in particular, it is not easy to compute equivalent
closed-form expressions, but we can compute numerically the residual moveout
curves given the expression for
, which allowed the computation of closed-form expressions
for the residual moveout of the multiples in both SODCIGs and ADCIGs. For
diffracted multiples in particular, it is not easy to compute equivalent
closed-form expressions, but we can compute numerically the residual moveout
curves given the expression for ![]() in terms of the
data-space coordinates (tm,hD,mD),
in terms of the
data-space coordinates (tm,hD,mD), ![]() and Xdiff. In principle,
the dip of the water-bottom can be estimated from the data and the position
of the diffractor corresponds to the lateral position of the apex of the
multiple diffraction in a shot gather as illustrated in the sketch of
Figure
and Xdiff. In principle,
the dip of the water-bottom can be estimated from the data and the position
of the diffractor corresponds to the lateral position of the apex of the
multiple diffraction in a shot gather as illustrated in the sketch of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
|
mul_sktch8
Figure 19 Sketch illustrating the raypaths of a diffracted multiple in a shot gather. The lateral position of the diffractor corresponds to the apex of the moveout curve. | 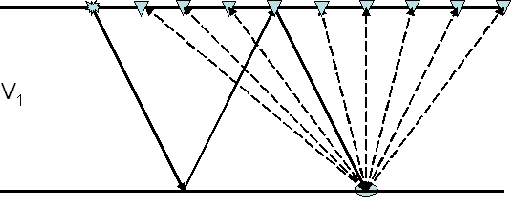 |