




Next: Real data example
Up: R. Clapp: Regularization
Previous: Large holes
A cost-effective implementation of fitting goals (2) or (4)
is challenging. The obvious domain to parallelize the inversion
is over frequency. In this case the model and data's time axis is log-stretched
nd transformed into the frequency domain. The resulting model
and data space are approximately three times their time domain
representation due to the oversampling necessitated by the log-stretch
operation.
In addition, both these volumes need to be transposed.
To apply the log-stretch FFT operation, the natural ordering is
for the time/frequency axis to be the inner axis while
the inversion is more efficient with the time/frequency axis
being the outer axis. An out-of-core transpose grows
in cost with the square of the number of elements.
For efficiency, I do a pre and post-step
parallel transpose of the data in conjunction with the
transformation to and from the log-stretched frequency domain.
I split the data long the 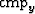 axis. For the pre-step
I log-stretch and FFT the input data, I then do an out-of-core
transpose of this smaller volume. I then collect the transposed
data. The post-step operation is simply the inverse, transpose
and then FFT and unstretch.
axis. For the pre-step
I log-stretch and FFT the input data, I then do an out-of-core
transpose of this smaller volume. I then collect the transposed
data. The post-step operation is simply the inverse, transpose
and then FFT and unstretch.
A second major problem is the number of iterations necessary
for convergence. The causal integration and leaky integration
are good preconditioners (fast convergence) but the AMO portion
tends to slow the inversion. As a result many (20-100 iterations)
are desirable. The global inversion approach described in
Clapp (2005b) is IO dominated. It also relies
on hardware stability. Both of these factors make a frequency-by-frequency
in-core inversion non-ideal but better choice. The
major drawback to a frequency by frequency approach is that
the frequencies might converge at significantly different rates
resulting in an image that is unrealistically dominated by
certain frequency ranges (most likely the low). To minimize
this problem, I stopped the inversion after a set reduction in
the data residual.
The final issue is the size of the problem. The domain
of 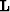 is four-dimensional and can be quite large even for
a relatively small model space. In addition, for a conjugate
gradient approach we still must keep three copies of our data space
(data, data residual, previous step data residual)
and five copies of our model space
(gradient, model, previous step, previous step model residual,
model residual). As a result, we need a machine with
significant memory and/or break the problem into patches in
the (
is four-dimensional and can be quite large even for
a relatively small model space. In addition, for a conjugate
gradient approach we still must keep three copies of our data space
(data, data residual, previous step data residual)
and five copies of our model space
(gradient, model, previous step, previous step model residual,
model residual). As a result, we need a machine with
significant memory and/or break the problem into patches in
the (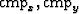 ) plane.
) plane.





Next: Real data example
Up: R. Clapp: Regularization
Previous: Large holes
Stanford Exploration Project
10/31/2005
![]() is four-dimensional and can be quite large even for
a relatively small model space. In addition, for a conjugate
gradient approach we still must keep three copies of our data space
(data, data residual, previous step data residual)
and five copies of our model space
(gradient, model, previous step, previous step model residual,
model residual). As a result, we need a machine with
significant memory and/or break the problem into patches in
the (
is four-dimensional and can be quite large even for
a relatively small model space. In addition, for a conjugate
gradient approach we still must keep three copies of our data space
(data, data residual, previous step data residual)
and five copies of our model space
(gradient, model, previous step, previous step model residual,
model residual). As a result, we need a machine with
significant memory and/or break the problem into patches in
the (![]() ) plane.
) plane.