




Next: Large holes
Up: R. Clapp: Regularization
Previous: R. Clapp: Regularization
Estimating a regularly sampled common-azimuth volume 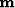 from our irregular input data
from our irregular input data 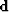 can be set up as a least squares inversion problem.
In this section, I will go over an approach to create
a common azimuth volume by setting up an inverse problem.
I will use a small synthetic to demonstrate the need for the various operators
in the inversion process.
can be set up as a least squares inversion problem.
In this section, I will go over an approach to create
a common azimuth volume by setting up an inverse problem.
I will use a small synthetic to demonstrate the need for the various operators
in the inversion process.
The data consists of irregular traces in a 5-D space (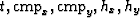 ).
The AMO operator acts on regularly sampled (
).
The AMO operator acts on regularly sampled (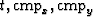 ) cubes, so we
map from the irregular data space to the regular model space
using a simple linear interpolation operator
) cubes, so we
map from the irregular data space to the regular model space
using a simple linear interpolation operator 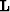 .
Figure
.
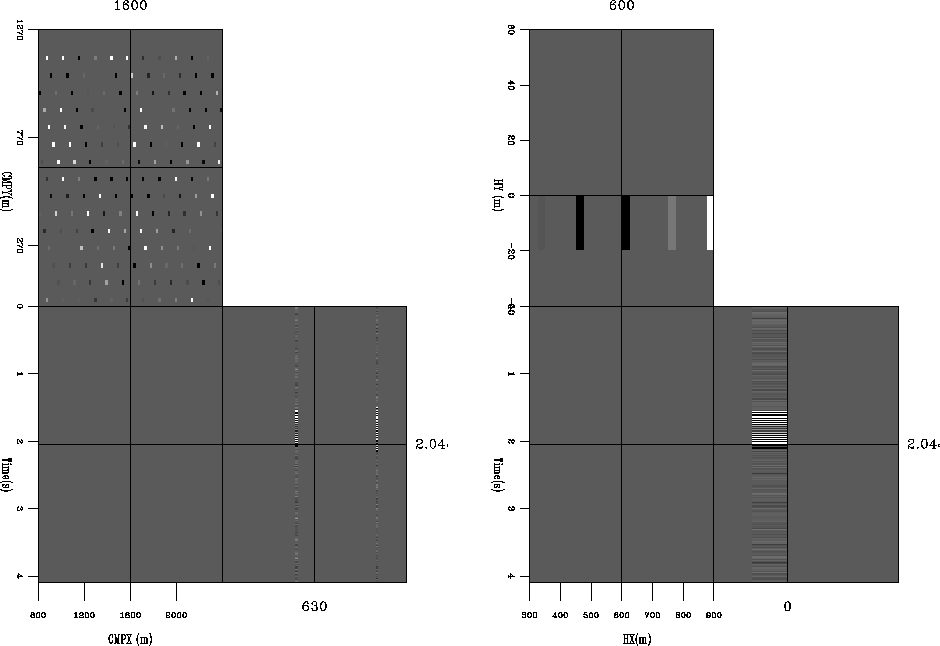
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two cube views from the five dimensional space the
data is mapped into. Notice the sparseness of the data in these cubes.
In standard marine acquisition, a single cross-line offset is acquired
for each midpoint. The standard multi-streamer acquisition results
in variation of the cross-line offset that is filled as we scan over
shows two cube views from the five dimensional space the
data is mapped into. Notice the sparseness of the data in these cubes.
In standard marine acquisition, a single cross-line offset is acquired
for each midpoint. The standard multi-streamer acquisition results
in variation of the cross-line offset that is filled as we scan over
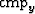 .
.
interp
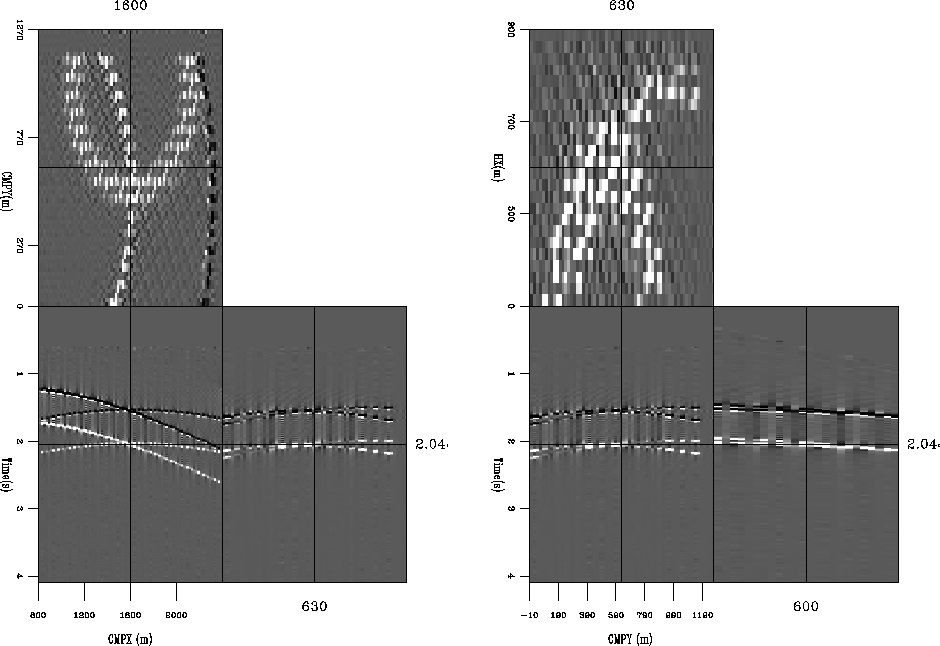
Figure 1 The location of the input traces for a simple
synthetic. The left panel is a constant offset cube (fixed hx and hy).
The right panel is a single midpoint (fixed 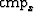 and and 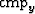 ). ).
|
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





For common azimuth migration, we want all of our data to reside at
hy=0. As a result, we need to use AMO to transform from the
hy that the data was recorded at to hy=0. The
operator  is a sum over the (
is a sum over the ( ) cubes
that have been transformed to hy=0.
Figure
) cubes
that have been transformed to hy=0.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two cube views of the result of applying
shows two cube views of the result of applying  to the
small synthetic. In this case we still have significant holes along
to the
small synthetic. In this case we still have significant holes along 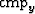 . I will
discuss why I created these holes later in the section.
. I will
discuss why I created these holes later in the section.
zero
Figure 2 The result of applying 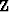 to the data
shown in Figure
to the data
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The left panel shows three slice from constant
offset cube. The right panel shows three slice from a constant
. The left panel shows three slice from constant
offset cube. The right panel shows three slice from a constant 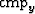 cube.
cube.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Finally, we need to add in our regularization term.
Generally, after NMO, our data should be smooth
as a function of offset. We can
think of adding a derivative operator along
the offset axis. We can improve this estimate
even further by applying a derivative on cubes
that have been transformed to the same offset using
AMO![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)
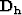 .We can write our fitting goals as
.We can write our fitting goals as
| 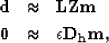 |
(1) |
| |
where  controls the importance
of consistency along the offset axis.
We can speed up the convergence of this
problem by preconditioning the model with
the inverse of our regularization operator.
In this case, we replace taking the derivative
of AMO cubes with performing causal integration
of AMO cubes
controls the importance
of consistency along the offset axis.
We can speed up the convergence of this
problem by preconditioning the model with
the inverse of our regularization operator.
In this case, we replace taking the derivative
of AMO cubes with performing causal integration
of AMO cubes 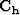 . Our new fitting goals then become
. Our new fitting goals then become
| 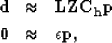 |
(2) |
| |
where 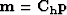 .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two cube views from the five dimensional space the
data is mapped into. Notice the sparseness of the data in these cubes.
In standard marine acquisition, a single cross-line offset is acquired
for each midpoint. The standard multi-streamer acquisition results
in variation of the cross-line offset that is filled as we scan over
shows two cube views from the five dimensional space the
data is mapped into. Notice the sparseness of the data in these cubes.
In standard marine acquisition, a single cross-line offset is acquired
for each midpoint. The standard multi-streamer acquisition results
in variation of the cross-line offset that is filled as we scan over

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif)