Independence of depth perturbations from angle perturbations

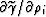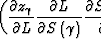In this appendix I demonstrate that the terms in equation 13 multiplying the partial derivatives with respect to the angles; that is, ${\partial \gamma}/{\partial \rho_{i}}$and ${\partial \widetilde{\gamma}}/{\partial \rho_{i}}$,are zero when evaluated at the point when the events are correctly migrated at zero subsurface offset. We are interested in estimating the RMO function measured for an incorrect velocity. That RMO function can be seen as a perturbation around the image obtained with the correct velocity.

After simple evaluation of partial derivatives the term multiplying 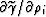${\partial \gamma}/{\partial \rho_{i}}$in equation 13 can be written as the following:

$$\begin{eqnarray} \left( \frac{\partial z_\gamma}{\partial L} \frac{\partial L}{\... ...}{\partial \gamma} + \tan \gamma-\tan \widetilde{\gamma} \right],\end{eqnarray}$$ (34)

that can be easily demonstrated to be equal to zero after substitution of the relationship between phase angles and group angles presented in equation 33.

The term multiplying 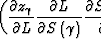${\partial \widetilde{\gamma}}/{\partial \rho_{i}}$is equal to

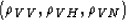$$\frac{\partial z}{\partial \widetilde{\gamma}} = -h_\xi\frac{1}{\cos ^2 \widetilde{\gamma}},$$ (35)

which is obviously equal to zero when the subsurface offset is zero, the point around which we are interested in expanding the RMO function. C