![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the geometry used to evaluate this impulse response.
illustrates the geometry used to evaluate this impulse response.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this concept and provide
the basis for computing the kinematics of the generalized migration operator.
illustrates this concept and provide
the basis for computing the kinematics of the generalized migration operator.
Since the transformation to ADCIGs operates
in the image space,
I analyze the spreading surfaces (impulse responses) of the generalized
prestack migration operator, which are defined in the image space.
In homogeneous anisotropic medium
the shape
of the impulse responses of
the generalized integral migration
can be easily evaluated analytically
as a function of the subsurface offset
![]() , in addition to the usual
image depth
, in addition to the usual
image depth ![]() and midpoint
and midpoint ![]() .Figure
.Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the geometry used to evaluate this impulse response.
illustrates the geometry used to evaluate this impulse response.
|
imp-resp
Figure 1 Geometry used for evaluating the impulse response of integral migration generalized to produce a prestack image function of the subsurface offset | 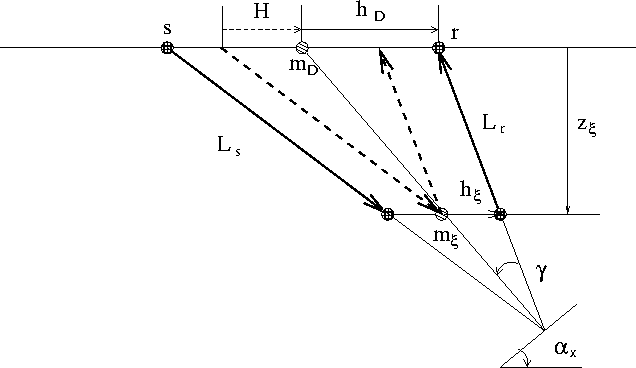 |
Assuming an arbitrary homogeneous anisotropic medium,
simple trigonometry applied to
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) allows us to express the impulse
response in parametric form, as a function of the
group dip angle
allows us to express the impulse
response in parametric form, as a function of the
group dip angle ![]() and the group aperture angle
and the group aperture angle ![]() .If we migrate an impulse recorded at time tD,
midpoint mD and surface offset hD,
the migration impulse response can be expressed as follows:
.If we migrate an impulse recorded at time tD,
midpoint mD and surface offset hD,
the migration impulse response can be expressed as follows:
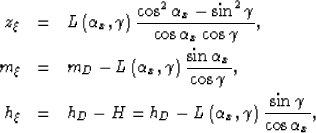 |
(1) | |
| (2) | ||
| (3) |
| |
(4) |
In 2-D, The ADCIGs are computed by applying a slant-stack decomposition on the prestack image along the subsurface offset axis, at constant midpoint. The kinematics of the transformation are defined by the following change of variables:
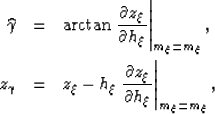 |
(5) | |
| (6) |
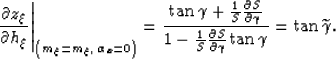 |
(7) |
Substituting equation 7 in equations 5 and 6 we obtain
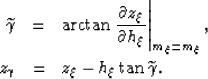 |
(8) | |
| (9) |
|
cig-2d-aniso-mva-flat-v1
Figure 2 Geometry of the transformation to the angle domain. The image point in the subsurface-offset domain | 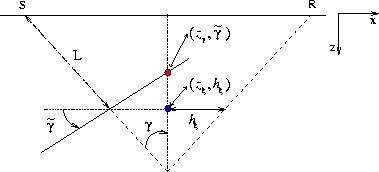 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) provides a geometrical interpretation
of the transformation to angle domain
of an image point with non-zero subsurface offset.
The transformation to angle domain moves the image point
in the subsurface-offset domain
provides a geometrical interpretation
of the transformation to angle domain
of an image point with non-zero subsurface offset.
The transformation to angle domain moves the image point
in the subsurface-offset domain ![]() to the image point in angle domain
to the image point in angle domain ![]() .The depth of the image point in angle domain
is determined by the intersection of the lines passing
through the points
.The depth of the image point in angle domain
is determined by the intersection of the lines passing
through the points
![]() and tilted by
and tilted by ![]() with respect to the horizontal.
When the migration velocity is correct,
and the image is fully focused at zero subsurface offset,
the transformation to angle domain does not change the depth
of the image point and the reflections are imaged at the
same depth for all aperture angles.
On the contrary, when the reflections are not focused at zero offset,
the transformation to angle domain maps the events at different depths
for each different angle.
The variability of the depth
with respect to the horizontal.
When the migration velocity is correct,
and the image is fully focused at zero subsurface offset,
the transformation to angle domain does not change the depth
of the image point and the reflections are imaged at the
same depth for all aperture angles.
On the contrary, when the reflections are not focused at zero offset,
the transformation to angle domain maps the events at different depths
for each different angle.
The variability of the depth ![]() with the aperture angle
is described by the RMO function that we want to measure
and quantify as a function of the perturbations
in anisotropic parameters encountered along the propagation paths.
with the aperture angle
is described by the RMO function that we want to measure
and quantify as a function of the perturbations
in anisotropic parameters encountered along the propagation paths.