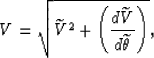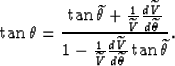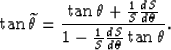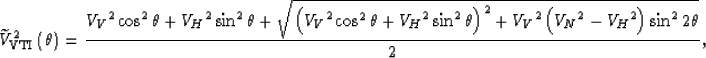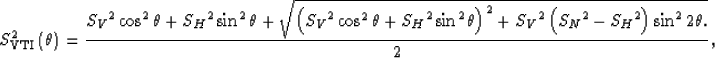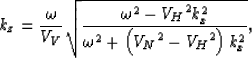Next: Angle Gathers by anisotropic
Up: Biondi: Anisotropic ADCIGs
Previous: Biondi: Anisotropic ADCIGs
In anisotropic wave propagation
the phase angles and velocities are different
from the group angles and velocities.
In this section I briefly review the concepts of phase and group
angles and velocities and the relationships between these
physical quantities.
I also define the particular approximation to a VTI medium that I use
in the numerical examples.
The transformation
from phase velocity 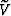 to group velocity V
is conventionally defined as the following
Tsvankin (2001):
to group velocity V
is conventionally defined as the following
Tsvankin (2001):
| 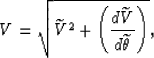 |
(1) |
where 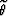 is the phase propagation angle.
The associated transformation from phase angles
to group angles
is the phase propagation angle.
The associated transformation from phase angles
to group angles 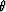 is defined
as:
is defined
as:
| 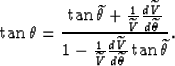 |
(2) |
Notice that throughout this paper I use the tilde
symbol to distinguish between phase quantities (with a tilde)
and group quantities (without a tilde).
Dellinger and Muir (1985) propose,
and heuristically motivate,
the following symmetric relations for the inverse transforms:
| 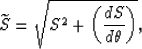 |
(3) |
where 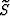 and S are respectively the phase slowness
and the group slowness,
and
and S are respectively the phase slowness
and the group slowness,
and
| 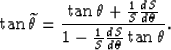 |
(4) |
I use the heuristic relation in equation 4
to derive some of the analytical results presented in this paper.
Furthermore, I use all the above relationships
to compute the kinematic numerical results presented
in this paper.
The numerical results, though not the analytical results,
are also dependent on the choice
of a specific approximation of the anisotropic
phase-velocity function.
I used the following VTI approximation for the phase velocity:
| 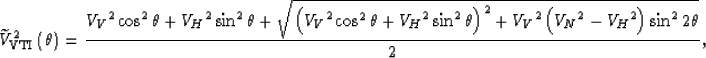 |
(5) |
where VV, VH, VN, are respectively
the vertical velocity, the horizontal velocity and the
NMO velocity.
Following Fowler (2003),
the corresponding approximation for the group velocity is
the following:
| 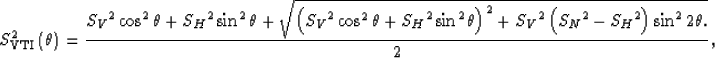 |
(6) |
where SV, SH, SN, are respectively
the vertical slowness, the horizontal slowness and the
NMO slowness.
The numerical results obtained by modeling and migrating
synthetic seismic data
and by migrating the real data
were obtained by source-receiver
depth continuation (upward for modeling and downward for migration)
using the following dispersion relation:
| 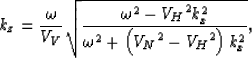 |
(7) |
where 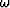 is the temporal frequency,
and kx and kz are respectively the horizontal and
vertical wavenumbers.
The dispersion relation shown in equation 7
corresponds to the velocity and slowness functions
in equations 5 and 6
Fowler (2003).
is the temporal frequency,
and kx and kz are respectively the horizontal and
vertical wavenumbers.
The dispersion relation shown in equation 7
corresponds to the velocity and slowness functions
in equations 5 and 6
Fowler (2003).





Next: Angle Gathers by anisotropic
Up: Biondi: Anisotropic ADCIGs
Previous: Biondi: Anisotropic ADCIGs
Stanford Exploration Project
11/1/2005
![]() to group velocity V
is conventionally defined as the following
Tsvankin (2001):
to group velocity V
is conventionally defined as the following
Tsvankin (2001):