![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). We choose a target zone (indicated with the "target" box in Figure
). We choose a target zone (indicated with the "target" box in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to see the effects of illumination on imaging close to the salt.
) to see the effects of illumination on imaging close to the salt.
The Sigsbee data set was modeled by simulating the geological setting found on the Sigsbee escarpment in the deep-water Gulf of Mexico. The model exhibits the illumination problems due to the complex salt shape, characterized by a rugose salt top (see Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). We choose a target zone (indicated with the "target" box in Figure
). We choose a target zone (indicated with the "target" box in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to see the effects of illumination on imaging close to the salt.
) to see the effects of illumination on imaging close to the salt.
 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the shot-profile migration image (using cross-correlation imaging condition) corresponding to the portion of Sigsbee model shown in figure
shows the shot-profile migration image (using cross-correlation imaging condition) corresponding to the portion of Sigsbee model shown in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Notice how the diffractor amplitudes located at 17000 feet depth fade away as they get closer to the salt. The same happens to the reflectors as they get close to the salt.
. Notice how the diffractor amplitudes located at 17000 feet depth fade away as they get closer to the salt. The same happens to the reflectors as they get close to the salt.
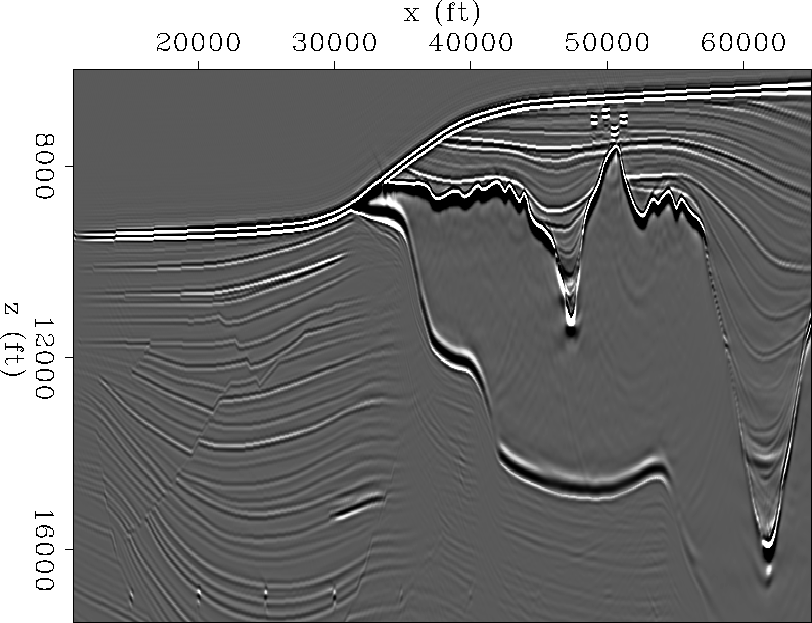 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a
shows a ![]() coefficient filter (target-oriented Hessian) at constant depth as the x coordinate moves from the sediments to the salt boundary. Figure
coefficient filter (target-oriented Hessian) at constant depth as the x coordinate moves from the sediments to the salt boundary. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows point 1, with coordinates
a shows point 1, with coordinates ![]() (far from the salt). Figure
(far from the salt). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b shows point 2, with coordinates
b shows point 2, with coordinates ![]() . Figure
. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c shows point 3, with coordinates
c shows point 3, with coordinates ![]() . Figure
. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d shows point 4, with coordinates
d shows point 4, with coordinates ![]() .
.
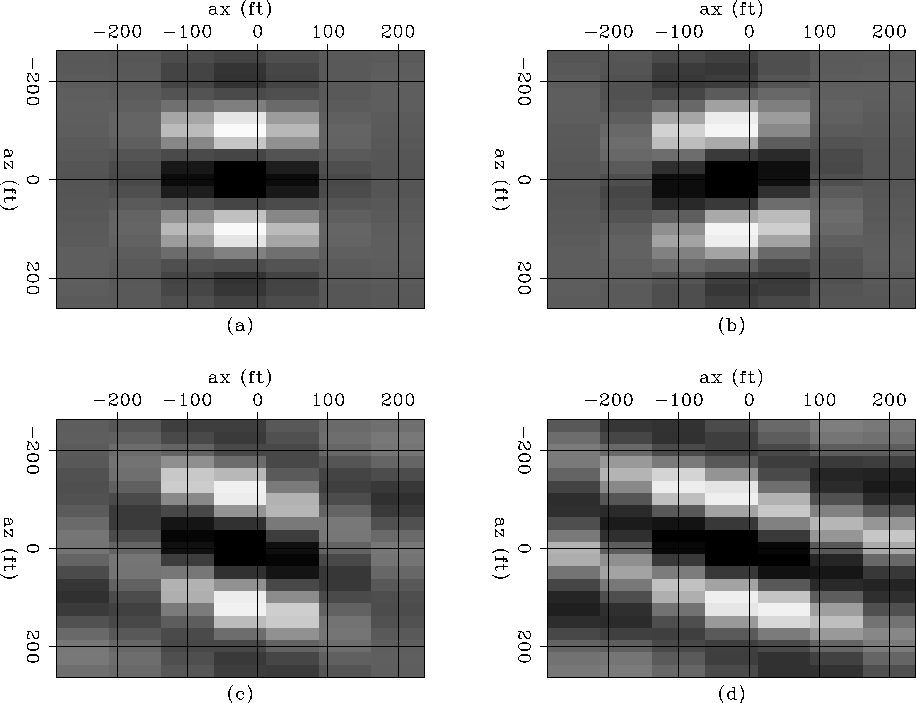 |
Unlike the constant velocity case Valenciano et al. (2005), the shape of the filter is not dependent only on the acquisition geometry but the subsurface geometry (presence of the salt body). In the area unaffected by the salt the filter looks the same as is the constant velocity case, but as we get closer to the salt the illumination varies (in intensity and angle) and the filter behaves differently. This is due to a focusing and defocusing effect created by the salt. To correct this effect we computed the least-squares inverse image, by the method described in Valenciano et al. (2005).
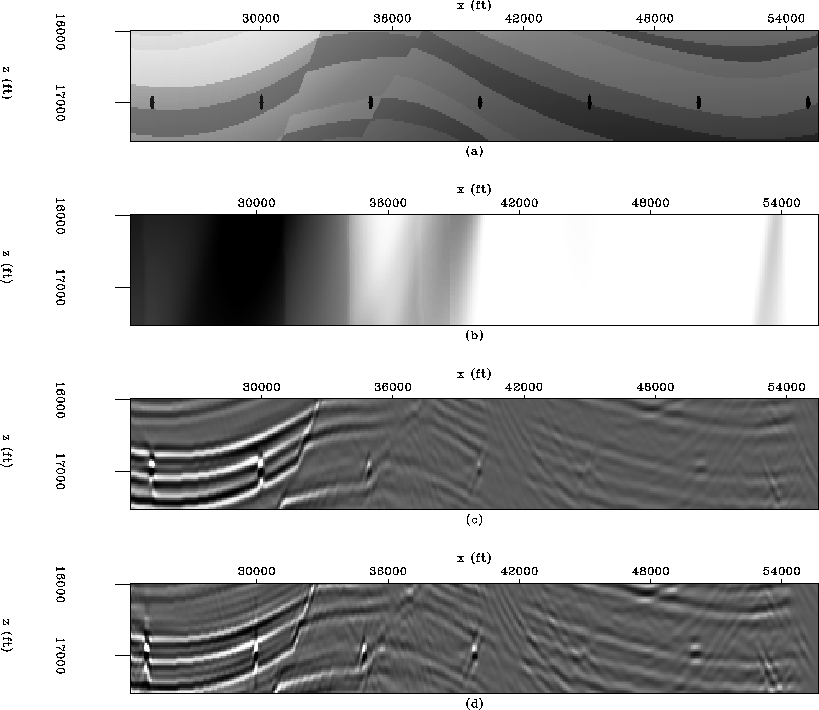
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a comparison between the migration and the inversion images in the target area. The stratigraphic model is shown in Figure
shows a comparison between the migration and the inversion images in the target area. The stratigraphic model is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. Notice the seven equal-strength point diffractors and the position of the faults. Figure
a. Notice the seven equal-strength point diffractors and the position of the faults. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b shows the illumination, which is the diagonal of the Hessian matrix (dark is high illumination light is low illumination). Notice the decrease in the illumination as it gets closer to the salt with the exception of a narrow strip where energy focuses close to the salt. The migration result is shown in Figure
b shows the illumination, which is the diagonal of the Hessian matrix (dark is high illumination light is low illumination). Notice the decrease in the illumination as it gets closer to the salt with the exception of a narrow strip where energy focuses close to the salt. The migration result is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c. The reflectors dim out as they get closer to the salt. In contrast, Figure
c. The reflectors dim out as they get closer to the salt. In contrast, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d shows the inversion result, the resolution increases (especially to the left of the image) and the section looks more balance. Also notice how the diffractors amplitude is better balanced.
d shows the inversion result, the resolution increases (especially to the left of the image) and the section looks more balance. Also notice how the diffractors amplitude is better balanced.
At the right of the image the resolution did not increase as much as to the left. This is due to the fact that data values (migration) to the left are bigger than to the right (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c), and so are the data residuals. Thus, the solver expends most of the time decreasing the residuals in that area.
c), and so are the data residuals. Thus, the solver expends most of the time decreasing the residuals in that area.
 |
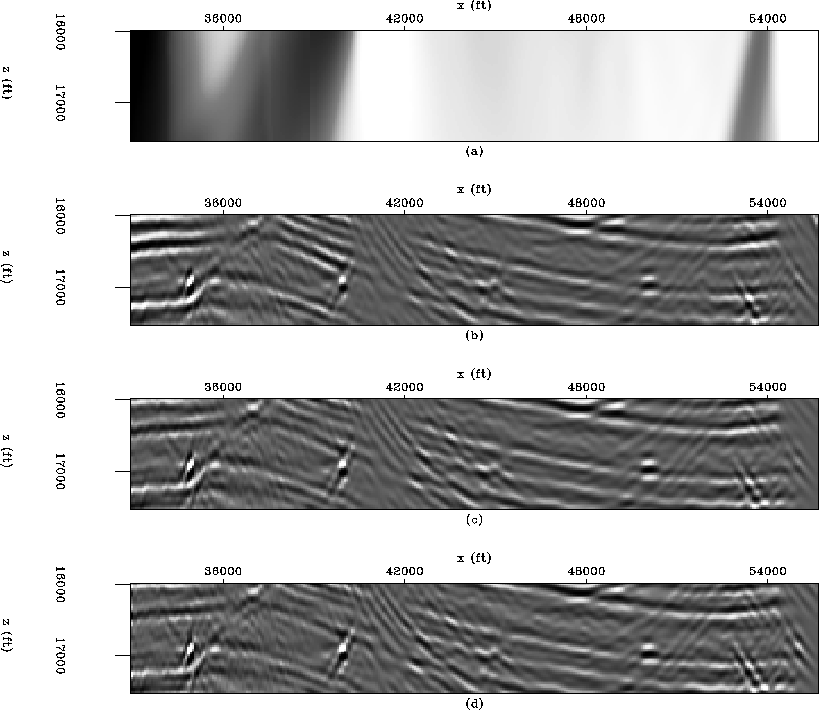 |
To test the previous hypothesis we did the inversion only in the low-illumination, reduced target area (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Figure
). Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the illumination (diagonal of the Hessian matrix) in the low-illumination area. Figure
a shows the illumination (diagonal of the Hessian matrix) in the low-illumination area. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b shows the migration in the low-illumination area. Figure
b shows the migration in the low-illumination area. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c shows the inversion performed in the full target area to match the dimensions of the inversion on the low-illumination area which is shown in Figure
c shows the inversion performed in the full target area to match the dimensions of the inversion on the low-illumination area which is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d.
There are substantial differences between the two inversion results: the result in the low-illumination area has better resolution than the one in the full target area, and the last diffractor (right corner) is more energetic in the result in the low-illumination than the one done in the full target area.
d.
There are substantial differences between the two inversion results: the result in the low-illumination area has better resolution than the one in the full target area, and the last diffractor (right corner) is more energetic in the result in the low-illumination than the one done in the full target area.
In general, even though inversion gives more balanced and better resolved images, it also produces more noisy results. Thus, a more sophisticated regularization might be necessary. Prucha et al. (2000) and Kuehl and Sacchi (2001) propose using a smoothing operator in the reflection angle (offset ray parameter) dimension. Valenciano and Biondi (2005) proposes a more general regularization in the reflection and azimuth angle dimensions.