Non-stationary least-squares filtering

The condition number of the target-oriented Hessian matrix can be high, making the solution of the non-stationary least-squares filtering problem in equation (5) unstable. One solution is adding a smoothing regularization operator to equation (5):

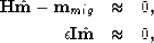$$\begin{eqnarray} {\bf H}\hat{{\bf m}}-{\bf m}_{mig}&\approx&0, \nonumber\\ \epsilon{\bf I}\hat{{\bf m}}&\approx&0, \end{eqnarray}$$ (6)

where the choice of the identity operator (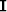${\bf I}$) as regularization operator is customary. A more sophisticated regularization scheme could involve applying a smoothing operator in the reflection angle (or offset ray-parameter) dimension Kuehl and Sacchi (2001); Prucha et al. (2000) or, more generally, in the reflection and azimuth angles as proposed by Valenciano and Biondi (2005).