Next: : REFERENCES
Up: Berryman: Geomechanical constants of
Previous: Appendix A: Effective Stress
One very common approximation made in studies of partially and patchy
saturated porous media (Norris, 1993; Mavko et al., 1998;
Johnson, 2001) is based on an assumption that the estimates
are being made over a small enough region that it is reasonable to
take the shear modulus of the porous frame as constant, even though the
bulk modulus over the same small region may vary. Then, when
Gassmann's results apply locally, the shear modulus satisfies
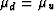 , and so remains constant throughout this same region
regardless of the distribution of fluids in the pores. When these
assumptions are valid, Hill's equation (3) may be used
to compute the effective bulk modulus K*, regardless of anisotropy
or of how many constituents might be present.
Furthermore, Hill's equation will apply
equally to the drained Kd* and undrained Ku* bulk moduli of
such a poroelastic system; Kn for the layers must be substituted
accordingly for the drained and undrained cases.
, and so remains constant throughout this same region
regardless of the distribution of fluids in the pores. When these
assumptions are valid, Hill's equation (3) may be used
to compute the effective bulk modulus K*, regardless of anisotropy
or of how many constituents might be present.
Furthermore, Hill's equation will apply
equally to the drained Kd* and undrained Ku* bulk moduli of
such a poroelastic system; Kn for the layers must be substituted
accordingly for the drained and undrained cases.
This approximation based on Hill's equation is very appealing for
applications because of its analytical beauty and overall simplicity,
but its use in heterogeneous media has never been
given a rigorous justification. In particular, the
assumption of variable bulk modulus in a heterogeneous
system having constant shear modulus is surely one worthy of careful
consideration. It seems more likely (at least to me)
that the variations in the bulk modulus in an earth system
will be mimicked by the shear modulus and, therefore, that the
proposed method is in truth an oversimplification of this complex
problem.
The model system presented here (i.e., the random polycrystal of porous
laminates) offers one means of checking whether
this use of Hill's equation might be justified or not.
It turns out that, when N = 2, Hill's equation (3)
can be inverted to give 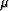 as a functional of K* (Milton, 1997).
The result is given by
as a functional of K* (Milton, 1997).
The result is given by
| 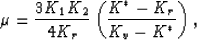 |
(30) |
where
| ![\begin{displaymath}
K_v = \sum_{n=1}^2 f_nK_n\qquad\hbox{and}\qquad
K_r = \left[\sum_{n=1}^2 \frac{f_n}{K_n}\right]^{-1}.
\end{displaymath}](img107.gif) |
(31) |
So I can do two calculations based on the results presented here for
heterogeneous systems. We can compute effective shear moduli
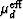 and
and 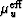 by taking the self-consistent values to be the true values of the
drained and undrained K*, and layer values of Kd(n) and Ku(n) as
the values for K1 and K2. The volume fractions are those
already used in these calculations. So everything is known and the
computations are straightforward. We want to check whether the resulting
values of effective shear moduli
by taking the self-consistent values to be the true values of the
drained and undrained K*, and layer values of Kd(n) and Ku(n) as
the values for K1 and K2. The volume fractions are those
already used in these calculations. So everything is known and the
computations are straightforward. We want to check whether the resulting
values of effective shear moduli
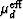 and
and 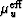 computed this way
are approximately constant and/or approximately equal to each other.
If they are, then Hill's equation, although not rigorously
appropriate in these systems, nevertheless could be capturing some of the
observed behavior. If this is not true, then the results would be
showing that great care should be exercised in using these formulas
for analyzing real data.
computed this way
are approximately constant and/or approximately equal to each other.
If they are, then Hill's equation, although not rigorously
appropriate in these systems, nevertheless could be capturing some of the
observed behavior. If this is not true, then the results would be
showing that great care should be exercised in using these formulas
for analyzing real data.
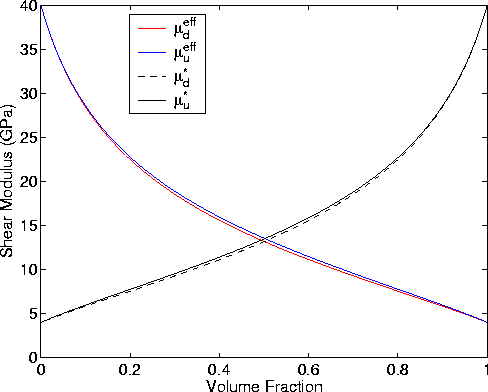
My results are illustrated in Figure 12. I find that 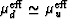 . However, except for the volume fractions near 50%,
the values of both
. However, except for the volume fractions near 50%,
the values of both 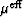 's are very different from the
actual shear moduli of the random polycrystals of porous laminates
model. The
's are very different from the
actual shear moduli of the random polycrystals of porous laminates
model. The 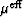 's are high when the
's are high when the 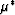 's are low, and vice
versa. This observation is a very strong negative result, showing that large
errors in analysis can be introduced for systems such as these that
are very heterogeneous in shear.
's are low, and vice
versa. This observation is a very strong negative result, showing that large
errors in analysis can be introduced for systems such as these that
are very heterogeneous in shear.
On the positive side, it is also clear from Figure 12 that if the spread
of layer 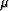 's is nonzero but small, then the use of Hill's equation
can be well justified. The error in shear estimates will never be greater than
the spread in the layer shear modulus values, so if this is a small (though
nonzero) number, then the errors will be finite but correspondingly small.
's is nonzero but small, then the use of Hill's equation
can be well justified. The error in shear estimates will never be greater than
the spread in the layer shear modulus values, so if this is a small (though
nonzero) number, then the errors will be finite but correspondingly small.
Fig12
Figure 12 Illustrating computations of an effective
shear modulus
obtained by inverting Hill's equation for drained (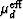 )and for undrained patchy saturation (
)and for undrained patchy saturation (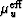 ) conditions.
Model parameters are the same as in Figure 9 for patchy saturation.
For comparison the curves for self-consistent shear moduli
) conditions.
Model parameters are the same as in Figure 9 for patchy saturation.
For comparison the curves for self-consistent shear moduli
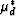 and
and 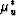 from Figure 10 are replotted here.
from Figure 10 are replotted here.






Next: : REFERENCES
Up: Berryman: Geomechanical constants of
Previous: Appendix A: Effective Stress
Stanford Exploration Project
5/3/2005
![]() as a functional of K* (Milton, 1997).
The result is given by
as a functional of K* (Milton, 1997).
The result is given by
![\begin{displaymath}
K_v = \sum_{n=1}^2 f_nK_n\qquad\hbox{and}\qquad
K_r = \left[\sum_{n=1}^2 \frac{f_n}{K_n}\right]^{-1}.
\end{displaymath}](img107.gif)
![]() . However, except for the volume fractions near 50%,
the values of both
. However, except for the volume fractions near 50%,
the values of both ![]() 's are very different from the
actual shear moduli of the random polycrystals of porous laminates
model. The
's are very different from the
actual shear moduli of the random polycrystals of porous laminates
model. The ![]() 's are high when the
's are high when the ![]() 's are low, and vice
versa. This observation is a very strong negative result, showing that large
errors in analysis can be introduced for systems such as these that
are very heterogeneous in shear.
's are low, and vice
versa. This observation is a very strong negative result, showing that large
errors in analysis can be introduced for systems such as these that
are very heterogeneous in shear.
![]() 's is nonzero but small, then the use of Hill's equation
can be well justified. The error in shear estimates will never be greater than
the spread in the layer shear modulus values, so if this is a small (though
nonzero) number, then the errors will be finite but correspondingly small.
's is nonzero but small, then the use of Hill's equation
can be well justified. The error in shear estimates will never be greater than
the spread in the layer shear modulus values, so if this is a small (though
nonzero) number, then the errors will be finite but correspondingly small.