Comparisons of conductivity bounds and estimates

We will now provide some comparisons like those presented in the previous section for elastic constant bounds and estimates.

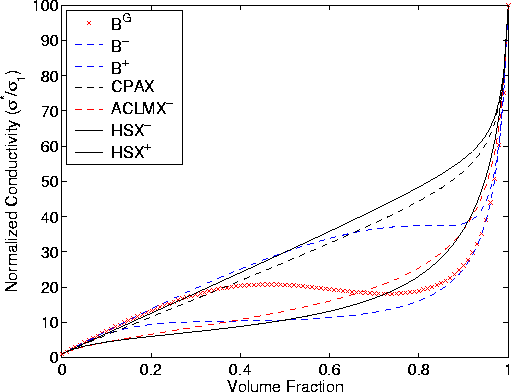
Figure 4 shows a comparison of (a) the correlated bounds of Hashin and Shtrikman (HSX$^\pm$) based on the random polycrystal microgeometry, (b) the microstructure-based bounds (assuming disk inclusions) of Beran (B$^\pm$), (c) the random polycrystal lower bounds of Avellaneda et al. (1988) [ACLMX^-] laminated (hexagonal symmetry) grains. A self-consistent (CPAX) estimate is based on the random polycrystal microstructure. A new estimator (B^G) is based on the Beran bounds and uses a geometric mean approximation in order to incorporate information contained in the microstructure constants $\zeta_i$.

 

volsigmaall
Figure 4 Conductivity comparisons.