Estimation schemes based on bounds for conductivity

The fundamental ideas used earlier to obtain estimates of elastic constants by using the analytical structure of the bounds (by making informed approximations for the elastic constants) can again be used for effective conductivity. The ideas are virtually the same, but somewhat easier to apply since we have only one constant to estimate, not two. Since we are now dealing with the Beran bounds on two-component media that depend specifically on the average 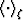$\left<\cdot\right\gt _\zeta$, we want to define again the geometric mean  

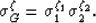$$\sigma_G^\zeta = \sigma_1^{\zeta_1}\sigma_2^{\zeta_2}.$$ (33)

Then we will have an estimator for a new transform variable that lies between the transform variables of the rigorous bounds according to  

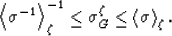$$\left<\sigma^{-1}\right\gt _\zeta^{-1} \le \sigma_G^\zeta \le \left<\sigma\right\gt _\zeta.$$ (34)

The properties of the canonical function 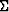$\Sigma$ guarantee that  

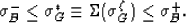$$\sigma_B^- \le \sigma_G^* \equiv \Sigma(\sigma_G^\zeta) \le \sigma_B^+.$$ (35)