2D Example - Canadian Foothills

The first test of the approach is on a 2D synthetic model characterized by rugged topography. This model is a merger of common geologic features from the Canadian Foothills in northeastern British Columbia, Canada Gray and Marfurt (1995). The velocity model, shown in Figure , consists of steep thrust fault planes and complex folds typical of a mountainous thrust region.

 

Foothills.vel Figure 2 Example of 2D topography from the Canadian Foothills. Topographic surface is the first break in gray tone from the surface.

The topographic boundary of interest is demarcated by the velocity model discontinuity nearest to the surface. The total relief of the model's surface is approximately 1600 m.

Figure  shows the test results. The flat datum surface is at a depth of 10000 m. Left-hand panels show the case where surface topography amplitudes are scaled down by 50$\%$.

 

Plot2D
Figure 3 Potential functions and coordinate systems generated for the Canadian Foothills velocity model. a) Potential function with topography scaled down by 50$\%$; b) Potential function with correct topography; c) coordinate system developed from the potential function of a); and d) coordinate system developed from the potential function of b). Note that increasing the amplitude of the topography tends to (de)focus the coordinate under topographic (lows) highs.

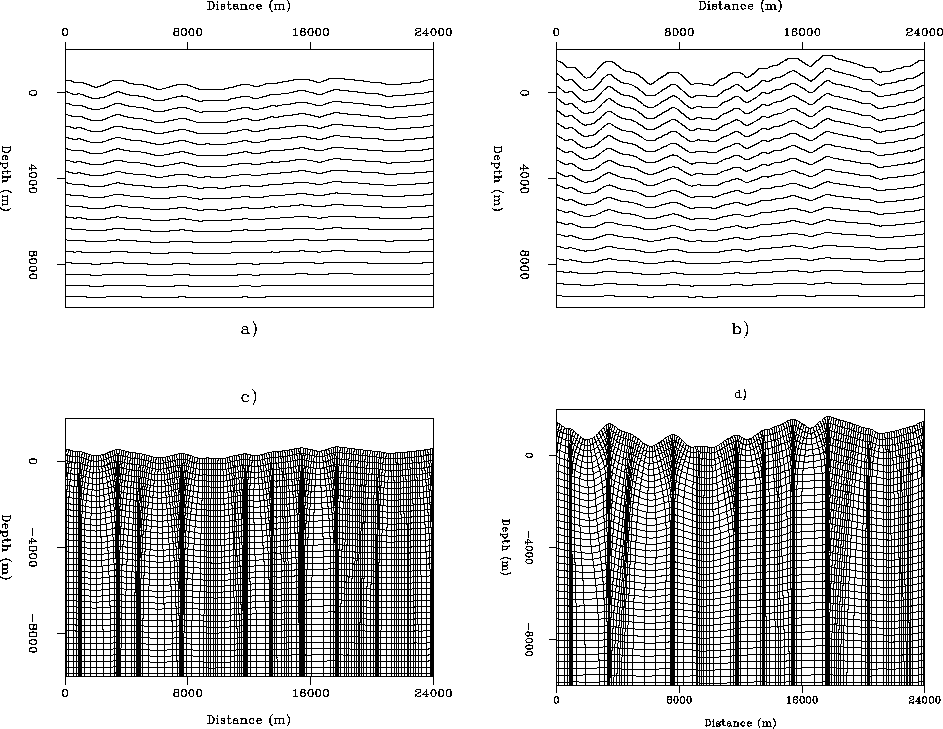The top left panel shows the 2-D potential function obtained through solution of Equation (5). The PF is rougher nearer the surface, but smooths out to become uniform at the lower domain boundary. The bottom left panel shows the coordinate system ray-traced from the PF presented in the top left panel. Note that the coordinate system focuses beneath topographic maxima, and defocuses under topographic minima. This demands that the Jacobian value in Equation (7) diverge from unity.

The right-hand panels of Figure  show results similar to those in the left-hand panels, except that the true topographic surface is restored. The top right panel shows a rougher PF, which is expected due to the increased topographic rugosity. The bottom right panel presents the coordinate system ray-traced from the PF shown in the upper right panel. Relative to that the bottom left panel, this coordinate system exhibits increased focusing and defocusing under topographic maxima and minima, respectively.