




Next: Sparse inversion
Up: Theory of noise attenuation
Previous: Theory of noise attenuation
In this section, we show the details of the linear radon transform and how it can be cast as an inverse problem. The forward transformation maps the radon
domain 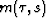 into the data space d(t,x) (recorded data) as
follows:
into the data space d(t,x) (recorded data) as
follows:
| 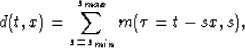 |
(2) |
and the adjoint transformation
| 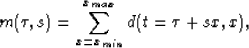 |
(3) |
where t is the time, x the station location
(xmin and xmax being the offset range),
s the slowness (smin and smax being the range of
slownesses investigated), and  the travel time at xmin
(the first trace is the origin of the summation path).
the travel time at xmin
(the first trace is the origin of the summation path).
Equation (2) can be rewritten in a more compact way by introducing
the forward linear radon transform operator L, the model space vector m (which
contains all the 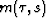 points) and the data vector d (which contains
all the d(t,x) points):
points) and the data vector d (which contains
all the d(t,x) points):
| 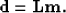 |
(4) |
Therefore, the goal is to minimize the difference between the input data
d and the modeled data via the linear radon transform operator as follows:
| 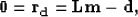 |
(5) |
where 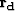 is called the data residual. As explained before,
the data are irregularly spaced and traces may be missing.
A mask
is called the data residual. As explained before,
the data are irregularly spaced and traces may be missing.
A mask 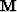 is introduced in equation (5) such
that only the recorded data are considered in the residual:
is introduced in equation (5) such
that only the recorded data are considered in the residual:
| 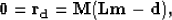 |
(6) |
where 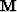 is a diagonal operator that equals one where
data are known and zero where they are unknown (at the
missing traces). Finally, we estimate the radon domain by
minimizing the objective function
is a diagonal operator that equals one where
data are known and zero where they are unknown (at the
missing traces). Finally, we estimate the radon domain by
minimizing the objective function
| 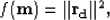 |
(7) |
which gives a least-squares estimate of the model parameters.
Note that with the linear radon transform, the model space 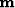 can be estimated without
inversion by introducing the so-called rho filter Yilmaz et al. (1987),
usually estimated in the Fourier domain. With missing traces, the rho
filter is not appropriate anymore and inversion is required.
In the next section, we describe how a sparse radon domain can be
estimated with inversion.
can be estimated without
inversion by introducing the so-called rho filter Yilmaz et al. (1987),
usually estimated in the Fourier domain. With missing traces, the rho
filter is not appropriate anymore and inversion is required.
In the next section, we describe how a sparse radon domain can be
estimated with inversion.





Next: Sparse inversion
Up: Theory of noise attenuation
Previous: Theory of noise attenuation
Stanford Exploration Project
5/3/2005
![]() points) and the data vector d (which contains
all the d(t,x) points):
points) and the data vector d (which contains
all the d(t,x) points):