|
alias-flat
Figure 7 Left panel shows the wavenumber energy for a migrated flat reflector when using sources at every tenth receiver location. On the left, and all source locations. | 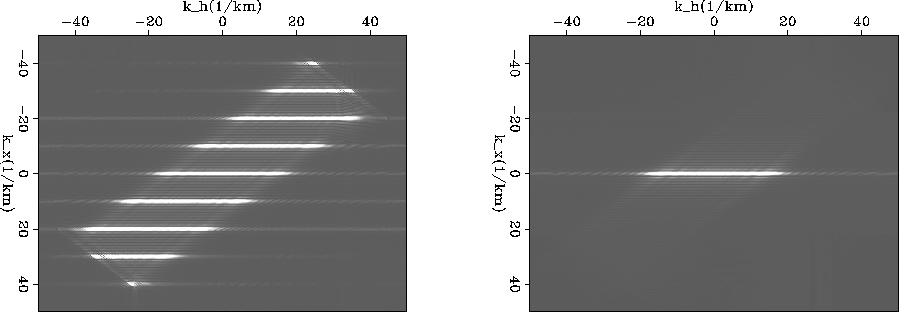 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the impact on the image space of
subsampling the shot axis by a factor of ten while migrating the flat
reflector synthetic data described above. The left panel imaged with
only every tenth shot, while right panel migrated shots at every
receiver location. The shot-axis, which could be drawn at a
45o angle up and to the right, shows inappropriate replications
Rickett and Sava (2002). The data are modeled with sufficient
receiver density, that this level of decimation does not alias the
receiver gathers. This is corroborated by the absence of aliased
energy in the upper-left and lower right quadrants.
shows the impact on the image space of
subsampling the shot axis by a factor of ten while migrating the flat
reflector synthetic data described above. The left panel imaged with
only every tenth shot, while right panel migrated shots at every
receiver location. The shot-axis, which could be drawn at a
45o angle up and to the right, shows inappropriate replications
Rickett and Sava (2002). The data are modeled with sufficient
receiver density, that this level of decimation does not alias the
receiver gathers. This is corroborated by the absence of aliased
energy in the upper-left and lower right quadrants.
|
alias-flat
Figure 7 Left panel shows the wavenumber energy for a migrated flat reflector when using sources at every tenth receiver location. On the left, and all source locations. |  |
From this simple example, we can see that the anti-aliasing restriction required for the decimated migration are sloped lines to remove energy from the upper-right and lower-left quadrants. In general, any of the four corners may experience aliased replications depending on the inequality between receiver and source sampling during acquisition. The form of the imaging condition in the Fourier domain as shown in equation 7 provides important insight into how to implement anti-aliasing criteria for shot-profile migration.
Limiting the image by neither constant kx nor kh will
appropriately remove the aliased energy of Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Instead, one should limit the maximum bandwidth
of both the
. Instead, one should limit the maximum bandwidth
of both the ![]() and
and ![]() wavefields. Table 1 provides a convenient display of
this fact. This will maintain the center diamond of appropriate energy. If the
anti-aliasing bandlimit is applied to the image space instead of the
two wavefields used to calculate it, there are two important
conclusions: 1) the bandlimit should be the same for both the offset
and location axes, and 2) the limit is a diamond shaped, not
circular, filter on the kx-kh plane.
wavefields. Table 1 provides a convenient display of
this fact. This will maintain the center diamond of appropriate energy. If the
anti-aliasing bandlimit is applied to the image space instead of the
two wavefields used to calculate it, there are two important
conclusions: 1) the bandlimit should be the same for both the offset
and location axes, and 2) the limit is a diamond shaped, not
circular, filter on the kx-kh plane.