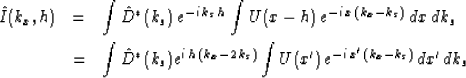Next: Synthetic tests
Up: Artman and Fomel: Fourier
Previous: Introduction
The space-domain shot-profile imaging condition including subsurface
offset for shot-profile migration Rickett and Sava (2002) is
| 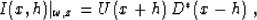 |
(1) |
Where I is the migrated image produced by cross-correlating the
up-coming, U, and down-going, D, wavefields at every depth and
frequency. Both x and h can be areal vectors. * represents
complex conjugation. To derive the Fourier-domain equivalent, we will
perform a piece-wise proof and begin with the Fourier transform D*
to 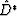 (neglecting Fourier scaling)
(neglecting Fourier scaling)
| 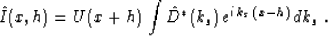 |
(2) |
Continue by Fourier transforming the variable x to find
| 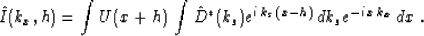 |
(3) |
By reordering variables, the equivalent form
| 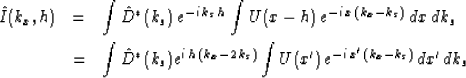 |
|
| (4) |
is achieved. From here, we can recognize the inner integral is the
Fourier transform of the wavefield U which can be replaced directly
to yield
| 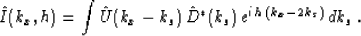 |
(5) |
With the use of the definition of offset, 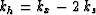 , we can
replace several of the above arguments with equivalent expressions to
find
, we can
replace several of the above arguments with equivalent expressions to
find
| 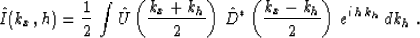 |
(6) |
The last integral is recognized as an inverse Fourier transform, this
time over the kh variable. Using this fact, we arrive at the
multi-dimensional (over x and h, which can be two-dimensional
themselves) Fourier transform of the general shot-profile imaging
condition
| 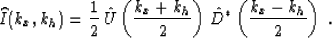 |
(7) |
From this equation, the result that the Fourier-domain equivalent to
the conventional space-domain imaging condition for shot-profile
migration is again a lagged multiplication of the up-coming and
down-going wavefields at each frequency and depth level. Evaluating
the arguments inside the wavefields to produce a component of the
image shows that the wavefields, in the wavenumber domain, will need
to be interpolated by a factor of two to calculate the image space
output. The Table 1 showing example calculations of the
components of the image space looks like
Table 1:
Layout of wavenumber components in Fourier-domain imaging conditions
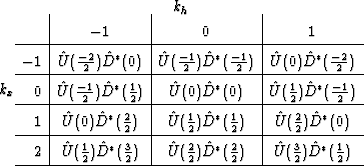 |





Next: Synthetic tests
Up: Artman and Fomel: Fourier
Previous: Introduction
Stanford Exploration Project
5/3/2005