Finding a model with simple bounds

In this section, I present the problem of finding simple bounds and the method that solves it.

The goal of bound-constrained optimization is to find a vector of model parameters 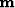${\bf m}$ such that we minimize  

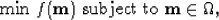$$\mbox{ min } f({\bf m})\mbox{ subject to }{\bf m}\in\Omega,$$ (1)

where

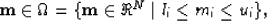$${\bf m}\in\Omega = \{ {\bf m} \in \Re^N\mid l_i\leq m_i\leq u_i\},$$ (2)

with l_i and u_i being the lower and upper bounds for the model m_i, respectively. In this case, l_i and u_i are called simple bounds. They can be different for each point of the model space. The model vector that obeys equation (1) is called 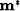${\bf m^*}$.

The sets of indices i for which the ith constraint are active/inactive are called the active/inactive sets A(m)/I(m). Most of the algorithms used to solve bound constrained problems first identify A(m) and then solve the minimization problem for the free variables of I(m).

 

• The L-BFGS-B algorithm