




Next: 2-D data examples
Up: Guitton et al.: Non-linear
Previous: Introduction
First consider a data volume d(x,y,z) where x and y
are the horizontal axes and z is the depth or time axis.
Building on Lomask (2003b), a vertical (time or depth) delay
function 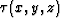 is estimated by minimizing the following
functional
is estimated by minimizing the following
functional 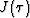 :
:
| ![\begin{displaymath}
J(\tau) = \int \int \left[ \left(p_x(x,y,z;\tau)-\frac{\part...
...u)-\frac{\partial
\tau}{\partial y}\right)^2 \right] \,dx\,dy,\end{displaymath}](img3.gif) |
(1) |
where px is the local step-out vector estimated in the x direction and
py is the local step-out vector estimated in the y direction. Both
vectors depend on  , which makes the problem of finding the time/depth
delays non-linear.
, which makes the problem of finding the time/depth
delays non-linear.
In this paper, we propose solving for 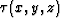 with a
quasi-Newton method called L-BFGS Guitton and Symes (2003). The
quasi-Newton method is an iterative process where the solution to the
problem is updated as follows:
with a
quasi-Newton method called L-BFGS Guitton and Symes (2003). The
quasi-Newton method is an iterative process where the solution to the
problem is updated as follows:
| 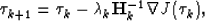 |
(2) |
where 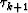 is the updated solution at iteration
k+1,
is the updated solution at iteration
k+1, 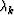 the step length computed by a line search
that ensures a sufficient decrease of
the step length computed by a line search
that ensures a sufficient decrease of 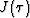 and
and
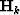 an approximation of the Hessian (or
second derivative.) One important property of L-BFGS is that it
requires the gradient of
an approximation of the Hessian (or
second derivative.) One important property of L-BFGS is that it
requires the gradient of 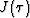 only to build the Hessian.
The gradient
only to build the Hessian.
The gradient 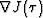 of
of 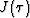 can be found by introducing the Euler-Lagrange equation and is given by:
can be found by introducing the Euler-Lagrange equation and is given by:
| 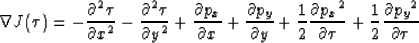 |
(3) |
The 2-D case is a simple extension of this result where the terms in
y are dropped. In practice, the last four terms of the gradient in
equation (3) can be precomputed and evaluated at
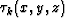 when needed for the BFGS update. This saves a lot of
computational effort. Note that the relative vertical (time or depth) delays are
computed with respect to a reference trace chosen a priori in the data
volume. A weight that would throw-out fitting equations at fault
locations can also be incorporated easily in both the gradient and
objective function.
when needed for the BFGS update. This saves a lot of
computational effort. Note that the relative vertical (time or depth) delays are
computed with respect to a reference trace chosen a priori in the data
volume. A weight that would throw-out fitting equations at fault
locations can also be incorporated easily in both the gradient and
objective function.
The most important components of this time/depth delay evaluation
technique are the dip fields px and py. In our implementation,
we use the method of Fomel (2002) to estimate both. This technique
estimates local dips from adjacent traces without slant-stacking.
It also gives one dip value only for each data point.
Next, 2-D and 3-D data examples illustrate the flattening technique.





Next: 2-D data examples
Up: Guitton et al.: Non-linear
Previous: Introduction
Stanford Exploration Project
5/3/2005
![]() with a
quasi-Newton method called L-BFGS Guitton and Symes (2003). The
quasi-Newton method is an iterative process where the solution to the
problem is updated as follows:
with a
quasi-Newton method called L-BFGS Guitton and Symes (2003). The
quasi-Newton method is an iterative process where the solution to the
problem is updated as follows: