Next: Mixed-domain solutions
Up: Theory
Previous: Theory
The space-domain finite-differences solution to equation (9)
is derived based on the square-root expansion,
first introduced to Geophysics by Muir
Claerbout (1985):
|  |
(10) |
where the coefficients  ,
,  and
and 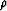 take the form:
take the form:
|  |
(11) |
In the special case of Cartesian coordinates,
a=s and b=1, equation (10) takes the familiar form
| 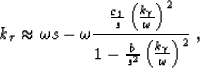 |
(12) |
where the coefficients c1 and b take different
values for different orders of the Muir expansion:
c15=(c1,b)=(0.50,0.00) for the 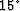 equation, and
c45=(c1,b)=(0.50,0.25) for the
equation, and
c45=(c1,b)=(0.50,0.25) for the  equation.
equation.





Next: Mixed-domain solutions
Up: Theory
Previous: Theory
Stanford Exploration Project
10/23/2004