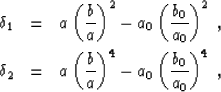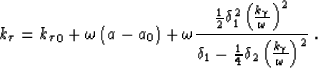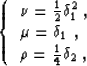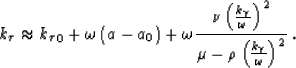Next: About this document ...
Up: Sava: Riemannian wavefield extrapolation
Previous: Mixed domain
The pseudo-screen solution to equation (9)
derives from a fourth-order expansion of the square-root
around (a0,b0) and (a,b):
| ![\begin{eqnarray}
k_\tau&\approx& \omega a \left [1+\frac{1}{2}\left (\frac{b k_\...
...ac{1}{8}\left (\frac{b_0k_\gamma}{a_0 \omega}\right )^4\right ]\;.\end{eqnarray}](img49.gif) |
|
| (30) |
If we subtract equations (30), we obtain:
| ![\begin{eqnarray}
k_\tau\approx {k_\tau}_0+ \omega\left (a-a_0\right )
&+&\frac{...
..._0}\right )^4\right ]\left (\frac{ k_\gamma}{ \omega}\right )^4\;.\end{eqnarray}](img50.gif) |
|
| (31) |
We can make the notations
| 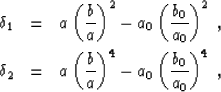 |
(32) |
| (33) |
therefore equation (31) becomes
| 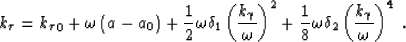 |
(34) |
With the approximation
| 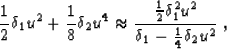 |
(35) |
we can write
| 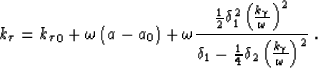 |
(36) |
If we make the notations
| 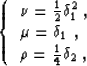 |
(37) |
we obtain the mixed-domain Fourier finite-differences
solution to the one-way wave equation in Riemannian coordinates:
| 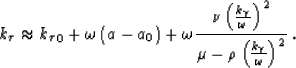 |
(38) |





Next: About this document ...
Up: Sava: Riemannian wavefield extrapolation
Previous: Mixed domain
Stanford Exploration Project
10/23/2004
![\begin{eqnarray}
k_\tau&\approx& \omega a \left [1+\frac{1}{2}\left (\frac{b k_\...
...ac{1}{8}\left (\frac{b_0k_\gamma}{a_0 \omega}\right )^4\right ]\;.\end{eqnarray}](img49.gif)
![\begin{eqnarray}
k_\tau&\approx& \omega a \left [1+\frac{1}{2}\left (\frac{b k_\...
...ac{1}{8}\left (\frac{b_0k_\gamma}{a_0 \omega}\right )^4\right ]\;.\end{eqnarray}](img49.gif)
![\begin{eqnarray}
k_\tau\approx {k_\tau}_0+ \omega\left (a-a_0\right )
&+&\frac{...
..._0}\right )^4\right ]\left (\frac{ k_\gamma}{ \omega}\right )^4\;.\end{eqnarray}](img50.gif)