Lost seismic energy and the fitting goals

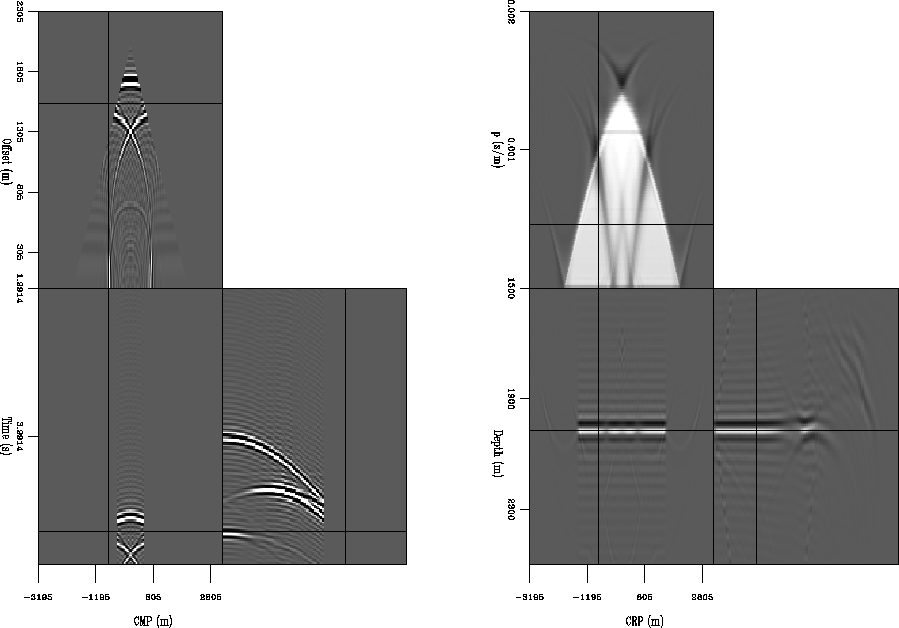
In a perfect world, we would have perfect data and the data fitting goal would allow us to construct a perfect model of the subsurface without needing any regularization. However, we never have perfect data. It is always corrupted by noise and the acquisition geometry is always a compromise between cost and what would provide sufficient data to image the subsurface. The latter is a particularly bad problem in areas of complex subsurface. Subsurface volumes with high velocity contrasts, such as salt bodies or even the simple low velocity lens model seen in Figure 1, are difficult to image at least partially due to seismic energy being directed outside of the limited survey area. The rays in Figure 1 show how seismic energy that is reflected at the flat reflector is affected by the low velocity lens. The maximum offset used in this paper is 4000 m, so the energy that is redirected by the lens will not be recorded. If we look at the synthetic data generated for this model (left panel of Figure 2), we can see the bounds of the survey cutting off the recorded events. The energy that leaves the survey bounds causes the migration result (right panel of Figure 2) to have holes in the common image gathers (CIGs).

Figure 2 indicates that we need to reconsider our fitting goals. Our model is incomplete because we are missing data. If we include the data that leaves the survey (${\bf d_L}$), our fitting goals become:

Initially, ${\bf d_L}$ is set to zero, since by definition we haven't recorded it. However, as we perform conjugate-gradient iterations of the fitting goals, regularizing the model with each iteration, we are filling in the parts of the model that correspond to ${\bf d_L}$ and thereby reconstructing some version of ${\bf d_L}$.

In practice, RIP includes ${\bf d_L}$ by padding the original data space with zero traces. However, since we are doing conjugate-gradient iterations, it is important to mask out the padded traces during each iteration. Otherwise the ``recovered'' ${\bf d_L}$ would exist in the data residual space and confuse the minimization. Defining

$${\bf d_{pad}}\ =\ \left[\begin{array} {c} {\bf d} \\ {\bf d_{L}} \\ \end{array}\right]$$ (4)

and including the weighting operator ${\bf W}$, the fitting goals become:

$$\begin{eqnarray} {\bf 0} & \approx & {\bf W}\left({\bf LA^{-1}p}\ -\ {\bf d_{pad}}\right) \\ {\bf 0} & \approx & \epsilon {\bf p}. \nonumber\end{eqnarray}$$ (5)

 

symesray Figure 1 Velocity model with a flat reflector under a low velocity lens. The maximum offset used for this experiment is 4000 m, so some of the rays representing seismic energy are directed outside of the survey bounds. Synthetic provided by Bill Symes and The Rice Inversion Project.

 

dat.mig
Figure 2 Left: The recorded data displayed as a flattened cube. The top panel is a time slice, the lower left is a common offset section and the lower right is a CMP gather. The triangular shape seen in the time slice is caused by the limited survey geometry. Right: The migration result. The top panel is a depth slice, lower left is a common offset ray parameter section, and lower right is a CIG. Note the holes caused by illumination problems in the reflector.