




Next: APPENDIX B: Bounds of
Up: Berryman: Bounds on geomechanical
Previous: DISCUSSION
Hashin-Shtrikman-style bounds (Hashin and Shtrikman, 1962; 1963)
on the bulk and shear moduli of
isotropic random polycrystals composed of hexagonal grains
have been derived by Peselnick and Meister (1965), with later corrections by Watt and Peselnick (1980) The main results are presented here
using notation consistent with that of our text, in order to
emphasize the connections to the analysis presented.
To keep this summary brief, we will merely quote the results
and refer the reader to the original papers for the derivations.
Parameters used to optimize the Hashin-Shtrikman bounds are
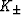 and
and 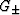 , which have the significance of being the bulk and shear
moduli of two isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Formulas for the bounds are:
, which have the significance of being the bulk and shear
moduli of two isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Formulas for the bounds are:
| 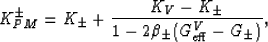 |
(17) |
and
| 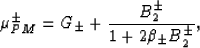 |
(18) |
where
| 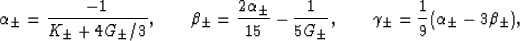 |
(19) |
and
| ![\begin{displaymath}
B_2^\pm = \frac{1}{5}\big[\frac{G_{\rm eff}^V - G_\pm}{{\cal...
...)} + \frac{2(c_{66}-G_\pm)}{1-2\beta_\pm(c_{66}-G_\pm)}\big],
\end{displaymath}](img71.gif) |
(20) |
with
| 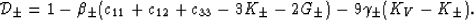 |
(21) |
Optimum values of the moduli for the comparison materials have been
shown to be (in our notation)
| 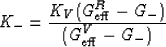 |
(22) |
with
| 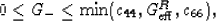 |
(23) |
and
| 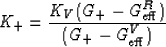 |
(24) |
with
| 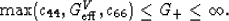 |
(25) |
Note that, when G- = 0, K- = KR, because
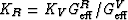 from the product formulas (Berryman, 2004). Also, note that, if Kn = K is constant, then
from the product formulas (Berryman, 2004). Also, note that, if Kn = K is constant, then
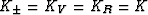 for any choice of
for any choice of 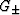 , since
then we also have that
, since
then we also have that 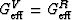 .
.
For the laminated materials considered here, the minimum condition in
(23) will never be satisfied by c66 except in the
trivial case of constant shear modulus. Each of the other two arguments
can possibly become the minimum under certain
nontrivial circumstances. For the materials considered here,
it follows from (7) that the maximum condition in
(25) will always be uniquely satisfied by c66, except
again for the trivial case of constant shear modulus.
Peselnick and Meister (1965) had originally obtained all
the results here except for the additional condition in
(23) that permits c44 to be replaced in certain
circumstancs by 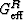 . This new condition was added later
by Watt and Peselnick (1980).
. This new condition was added later
by Watt and Peselnick (1980).





Next: APPENDIX B: Bounds of
Up: Berryman: Bounds on geomechanical
Previous: DISCUSSION
Stanford Exploration Project
10/23/2004
![]() and
and ![]() , which have the significance of being the bulk and shear
moduli of two isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Formulas for the bounds are:
, which have the significance of being the bulk and shear
moduli of two isotropic comparison materials. G+,K+ are the values
used in the formulas for the upper bounds, and G-,K- for the lower bounds.
Formulas for the bounds are:
![]() . This new condition was added later
by Watt and Peselnick (1980).
. This new condition was added later
by Watt and Peselnick (1980).