




Next: FORMATION FACTOR BOUNDS
Up: Berryman: Bounds on transport
Previous: INTRODUCTION
The Bergman-Milton
(Bergman, 1978, 1980; Milton, 1980, 1981; Bergman, 1982; Korringa and
LaTorraca, 1986; Stroud et al., 1986; Berryman, 1992)
analytical approach to understanding some generic effective
conductivity g* of two-component inhomogeneous media shows that
| 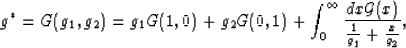 |
(1) |
where G(1,0) and G(0,1) are constants depending only on the geometry and
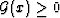 is a resonance density also depending only on the
geometry. The integral in (1) is known as a
Stieltjes integral (Baker, 1975). Although the representation
(1) has usually been employed to study the
behavior of g* in the complex plane
when g1 and g2 are themselves complex (corresponding to mixtures of
conductors and dielectrics), I will restrict consideration here - as
Bergman did in his early work (Bergman, 1978) - to pure
conductors so that g1, g2, and g* are all real and nonnegative.
is a resonance density also depending only on the
geometry. The integral in (1) is known as a
Stieltjes integral (Baker, 1975). Although the representation
(1) has usually been employed to study the
behavior of g* in the complex plane
when g1 and g2 are themselves complex (corresponding to mixtures of
conductors and dielectrics), I will restrict consideration here - as
Bergman did in his early work (Bergman, 1978) - to pure
conductors so that g1, g2, and g* are all real and nonnegative.
In the limit that one or the other of the two constituents is a perfect
insulator (gi = 0), or in the more common case when one of the
constituents is much more strongly conducting than the other, I can
define two quantities called formation factors (Archie, 1942)
by
| 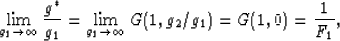 |
(2) |
and, similarly, by
| 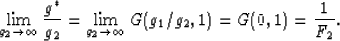 |
(3) |
In a porous material, where solid and pore fluid are each
continuously connected throughout the material, both formation
factors are finite, and both satisfy 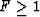 . The more commonly
measured quantity of this type is the electrical formation factor
for the continuous fluid component. This measurement has some
possible complications due to surface conductance
(Johnson et al., 1986; Wildenschild et al., 2000),
but it is usually not contaminated by
conductance through the bulk solid material because most rock grains can be
correctly assumed to be electrically insulating to a very good
approximation. Since the formation factor is strictly a measure
of the microgeometry of the heterogeneous medium, it is the same number
[except for those possible complications already mentioned
of surface electrical conduction
(Johnson et al., 1986; Wildenschild et al., 2000),
which can be eliminated whenever necessary by known experimental
methods] for all mathematically equivalent conductivities.
For this presentation, I will use F1 to represent this formation
factor associated with the pore space. On the other hand,
for thermal conduction the rock grains are the most highly conducting
component and the pore fluids tend to be much more poorly conducting -
especially so in the case of saturating air. So I will take F2 to be
this formation factor associated with the solid frame of the porous material.
. The more commonly
measured quantity of this type is the electrical formation factor
for the continuous fluid component. This measurement has some
possible complications due to surface conductance
(Johnson et al., 1986; Wildenschild et al., 2000),
but it is usually not contaminated by
conductance through the bulk solid material because most rock grains can be
correctly assumed to be electrically insulating to a very good
approximation. Since the formation factor is strictly a measure
of the microgeometry of the heterogeneous medium, it is the same number
[except for those possible complications already mentioned
of surface electrical conduction
(Johnson et al., 1986; Wildenschild et al., 2000),
which can be eliminated whenever necessary by known experimental
methods] for all mathematically equivalent conductivities.
For this presentation, I will use F1 to represent this formation
factor associated with the pore space. On the other hand,
for thermal conduction the rock grains are the most highly conducting
component and the pore fluids tend to be much more poorly conducting -
especially so in the case of saturating air. So I will take F2 to be
this formation factor associated with the solid frame of the porous material.





Next: FORMATION FACTOR BOUNDS
Up: Berryman: Bounds on transport
Previous: INTRODUCTION
Stanford Exploration Project
10/23/2004