




Next: Conclusion
Up: Shan and Biondi: Anisotropic
Previous: Explicit correction operator
The performance of an extrapolation operator can be verified by its impulse response.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are
the impulse responses of the qP-wave in the same medium using three different methods.
The symmetry axis of the medium is tilted
are
the impulse responses of the qP-wave in the same medium using three different methods.
The symmetry axis of the medium is tilted 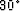 from the vertical direction.
The qP- and qSV-wave velocities in the direction parallel to the symmetry axis
are 2000 m/s and 1100 m/s, respectively.
The anisotropic parameters
from the vertical direction.
The qP- and qSV-wave velocities in the direction parallel to the symmetry axis
are 2000 m/s and 1100 m/s, respectively.
The anisotropic parameters  and
and 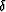 are 0.4 and 0.2, respectively.
The impulse location is at 4000 m.
are 0.4 and 0.2, respectively.
The impulse location is at 4000 m.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the impulse response of isotropic phase-shift with an
anisotropic correction operator. Figure
is the impulse response of isotropic phase-shift with an
anisotropic correction operator. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the impulse
response of isotropic FFD with an anisotropic correction operator. The reference
velocity for the FFD is 1500 m/s. We use 39 points for the explicit correction operator in Figures
is the impulse
response of isotropic FFD with an anisotropic correction operator. The reference
velocity for the FFD is 1500 m/s. We use 39 points for the explicit correction operator in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Since the medium is homogeneous, we can also extrapolate the wavefield with anisotropic phase-shift (equation (5)).
Figure
.
Since the medium is homogeneous, we can also extrapolate the wavefield with anisotropic phase-shift (equation (5)).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the impulse response of anisotropic phase-shift.
Comparing Figures
is the impulse response of anisotropic phase-shift.
Comparing Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the impulse response of the isotropic operator with an anisotropic correction operator
is the same as that of the anisotropic phase-shift method for propagating angles up to almost
,
the impulse response of the isotropic operator with an anisotropic correction operator
is the same as that of the anisotropic phase-shift method for propagating angles up to almost 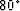 .It is different from anisotropic phase-shift for higher angles because the explicit
correction operator is not same as the one for anisotropic phase-shift for wavenumbers close to
the evanescent area.
.It is different from anisotropic phase-shift for higher angles because the explicit
correction operator is not same as the one for anisotropic phase-shift for wavenumbers close to
the evanescent area.





Next: Conclusion
Up: Shan and Biondi: Anisotropic
Previous: Explicit correction operator
Stanford Exploration Project
10/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the impulse response of isotropic phase-shift with an
anisotropic correction operator. Figure
is the impulse response of isotropic phase-shift with an
anisotropic correction operator. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the impulse
response of isotropic FFD with an anisotropic correction operator. The reference
velocity for the FFD is 1500 m/s. We use 39 points for the explicit correction operator in Figures
is the impulse
response of isotropic FFD with an anisotropic correction operator. The reference
velocity for the FFD is 1500 m/s. We use 39 points for the explicit correction operator in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Since the medium is homogeneous, we can also extrapolate the wavefield with anisotropic phase-shift (equation (5)).
Figure
.
Since the medium is homogeneous, we can also extrapolate the wavefield with anisotropic phase-shift (equation (5)).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the impulse response of anisotropic phase-shift.
Comparing Figures
is the impulse response of anisotropic phase-shift.
Comparing Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
the impulse response of the isotropic operator with an anisotropic correction operator
is the same as that of the anisotropic phase-shift method for propagating angles up to almost
,
the impulse response of the isotropic operator with an anisotropic correction operator
is the same as that of the anisotropic phase-shift method for propagating angles up to almost