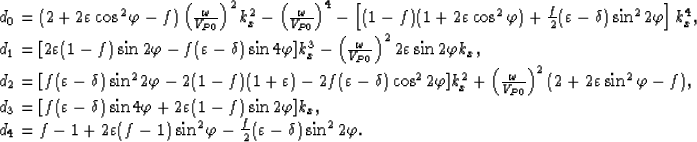Next: Extrapolation operator in laterally
Up: Shan and Biondi: Anisotropic
Previous: Introduction
In a VTI media, the phase velocity of qP- and qSV-waves in Thomsen's notation can be expressed as Tsvankin (1996):
| 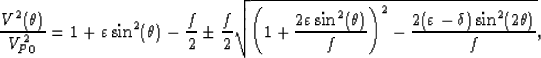 |
(1) |
where 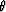 is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0 are the qP- and qSV- wave velocities in the vertical direction, respectively.
is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0 are the qP- and qSV- wave velocities in the vertical direction, respectively.
 and
and 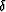 are anisotropy parameters defined by Thomsen (1986):
are anisotropy parameters defined by Thomsen (1986):
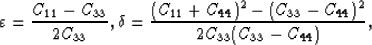
where Cij are elastic moduli.
In equation (1), 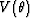 the is qP-wave phase-velocity when the sign in front of the square root is positive,
and the qSV-wave phase velocity for a negative sign.
the is qP-wave phase-velocity when the sign in front of the square root is positive,
and the qSV-wave phase velocity for a negative sign.
If we rotate the symmetry axis from vertical to a tilted angle 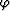 , we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle
, we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle 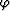 with the vertical direction:
with the vertical direction:
| 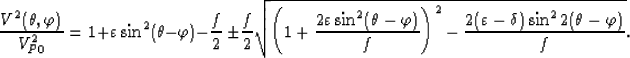 |
(2) |
Here, in contrast to equation (1),  and
and 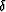 are now defined in a direction tilted by the angle
are now defined in a direction tilted by the angle
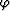 from the vertical direction. VP0 is the qP-wave velocity in the direction parallel to the symmetry axis.
from the vertical direction. VP0 is the qP-wave velocity in the direction parallel to the symmetry axis.
For plane-wave propagation, the phase angle 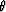 is related to the wavenumbers kx and kz by:
is related to the wavenumbers kx and kz by:
|  |
(3) |
where 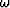 is the temporal frequency. Squaring equation (2) and substituting (3) into (2), we
can obtain a dispersion relation equation:
is the temporal frequency. Squaring equation (2) and substituting (3) into (2), we
can obtain a dispersion relation equation:
|
d4kz4+d3kz3+d2kz2+d1kz+d0=0,
|
(4) |
where the coefficients d0,d1,d2,d3, and d4 are as follows:
The dispersion relation equation (4) is a quartic equation. It can be solved analytically Abramowitz and Stegun (1972) or
numerically by Newton's Method Stoer and Bulirsch (1992). Equation (4) has four roots, which are related to up-going and down-going
qP- and qSV- waves, respectively. For a medium without lateral change in the velocity VP0 and anisotropy parameters
 and
and  , the wavefield can be extrapolated by the phase-shift method Gazdag (1978):
, the wavefield can be extrapolated by the phase-shift method Gazdag (1978):
| 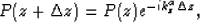 |
(5) |
where kza is one of the roots of equation (4).





Next: Extrapolation operator in laterally
Up: Shan and Biondi: Anisotropic
Previous: Introduction
Stanford Exploration Project
10/23/2004
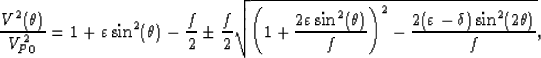
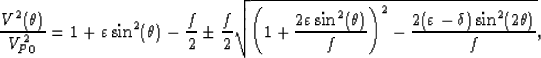
![]()
![]() , we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle
, we obtain the phase velocity of
a tilted TI medium whose symmetry axis forms an angle ![]() with the vertical direction:
with the vertical direction:
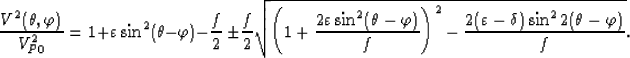
![]() is related to the wavenumbers kx and kz by:
is related to the wavenumbers kx and kz by: