




Next: The L-BFGS-B algorithm
Up: Optimization
Previous: Gradient Projection Algorithm
Trust region methods are widely popular for solving problems where
the Hessian has regions of negative curvatures Kelley (1999).
The basic idea behind these methods is to fit the objective function
locally with a quadratic model near a point 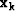 :
:
| 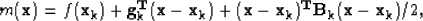 |
(5) |
where 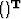 is the transpose and
is the transpose and 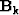 is the Hessian
of
is the Hessian
of 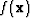 at iteration k. The goal is to find an
at iteration k. The goal is to find an  that minimizes
that minimizes  such that
such that
| 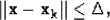 |
(6) |
where  is the trust region radius. Once a local minimizer is
found, either the step is accepted, or the radius
is the trust region radius. Once a local minimizer is
found, either the step is accepted, or the radius  is changed,
or both. Termination criterion end the process. In the most simple
case, an update of
is changed,
or both. Termination criterion end the process. In the most simple
case, an update of 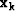 is obtained by minimizing the projected steepest
descent onto the quadratic area
is obtained by minimizing the projected steepest
descent onto the quadratic area
| 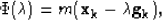 |
(7) |
with
This update is also called the Cauchy point.
This technique resembles quite closely the projection gradient
algorithm to find the active set  . It is then not surprising
that many algorithms for bound constrained optimization are
either completely or partially based on trust region methods.
. It is then not surprising
that many algorithms for bound constrained optimization are
either completely or partially based on trust region methods.
The algorithm used in this paper does not involve any trust region radii,
but line search algorithms instead. Yet, this algorithm keeps the concept of
fitting the objective function locally with a quadratic form in
equation (5) to find the minimum of 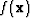 in
equation (1).
in
equation (1).





Next: The L-BFGS-B algorithm
Up: Optimization
Previous: Gradient Projection Algorithm
Stanford Exploration Project
10/23/2004
![]() in
equation (1).
in
equation (1).