




Next: 2-D Field Data Results
Up: Particular Implementation of LSJIMP
Previous: Velocity-Depth Ambiguity in the
Now that we have derived appropriate imaging and amplitude correction operators,
we are ready to translate the general LSJIMP modeling equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to my particular implementation. The primary image,
) to my particular implementation. The primary image,
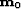 , is mapped into data space primary events by NMO,
, is mapped into data space primary events by NMO, 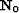 .
Similarly, a given pegleg image,
.
Similarly, a given pegleg image, 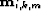 , is mapped into data space by
sequentially applying the differential geometric spreading correction
(
, is mapped into data space by
sequentially applying the differential geometric spreading correction
(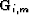 ), Snell resampling (
), Snell resampling (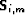 ), HEMNO (
), HEMNO (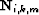 ),
and finally, a reflection coefficient (
),
and finally, a reflection coefficient (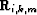 ). Let us rewrite
equation (
). Let us rewrite
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) accordingly:
) accordingly:
| 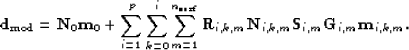 |
(28) |
We see that in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the analog to
), the analog to
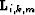 in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
) is
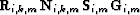 .
.
The data residual weight in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
), 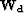 , can often
strongly influence the success of the inversion. Technically,
, can often
strongly influence the success of the inversion. Technically, 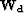 carries
a heavy burden: it must decorrelate and balance the residual. However, I have
found that a simpler form for
carries
a heavy burden: it must decorrelate and balance the residual. However, I have
found that a simpler form for 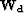 nontheless pays dividends. I set
nontheless pays dividends. I set
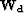 , which has the same dimension as a CMP gather, to zero where the data,
, which has the same dimension as a CMP gather, to zero where the data,
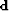 , has an empty trace, and also above the onset of the seabed reflection.
, has an empty trace, and also above the onset of the seabed reflection.





Next: 2-D Field Data Results
Up: Particular Implementation of LSJIMP
Previous: Velocity-Depth Ambiguity in the
Stanford Exploration Project
5/30/2004
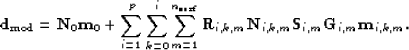
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to my particular implementation. The primary image,
) to my particular implementation. The primary image,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) accordingly:
) accordingly:
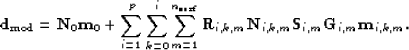
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the analog to
), the analog to
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
) is
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
), ![]() , can often
strongly influence the success of the inversion. Technically,
, can often
strongly influence the success of the inversion. Technically, ![]() carries
a heavy burden: it must decorrelate and balance the residual. However, I have
found that a simpler form for
carries
a heavy burden: it must decorrelate and balance the residual. However, I have
found that a simpler form for ![]() nontheless pays dividends. I set
nontheless pays dividends. I set
![]() , which has the same dimension as a CMP gather, to zero where the data,
, which has the same dimension as a CMP gather, to zero where the data,
![]() , has an empty trace, and also above the onset of the seabed reflection.
, has an empty trace, and also above the onset of the seabed reflection.