 |
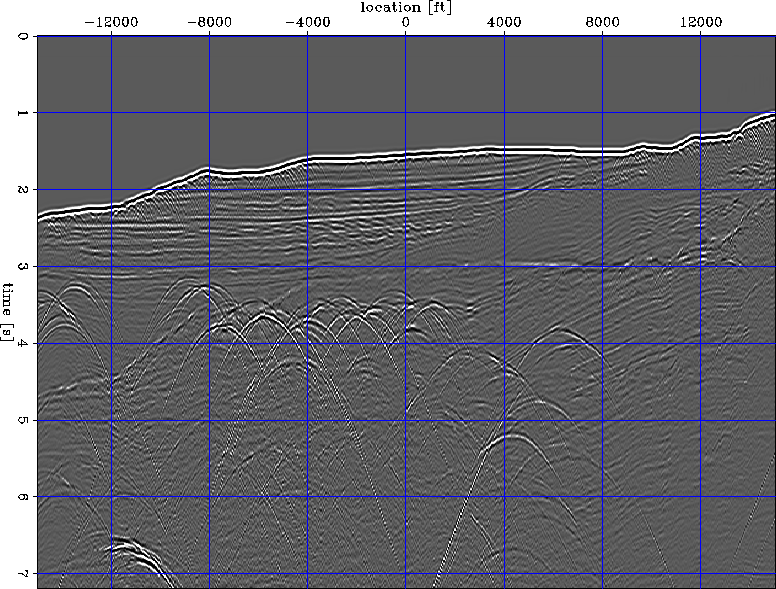
Figure 3 Zero-offset synthetic data used for focusing migration velocity analysis.
Figure 3 shows the zero-offset data we use for velocity analysis to delineate the top of the rough salt body. The section contains a large number of diffractors, whose focusing allows us to constrain the overburden velocity model.
 |
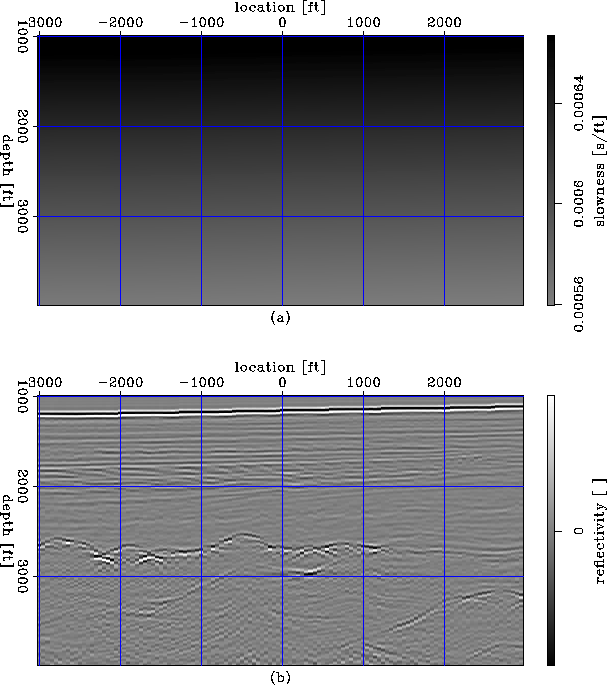
Figure 4(a) depicts the starting velocity model, and Figure 4(b) depicts the initial image obtained by zero-offset migration. The starting velocity is a typical Gulf of Mexico v(z) function hanging from the water bottom. Uncollapsed diffractions are visible at the top of the salt, indicating that the velocity in the overburden is not accurate. Such defocusing also hampers our ability to pick accurately the top of the salt and, therefore, degrades imaging at depth.
 |
As we did for the preceding synthetic example,
we run residual migration
on the background image (Figure 4).
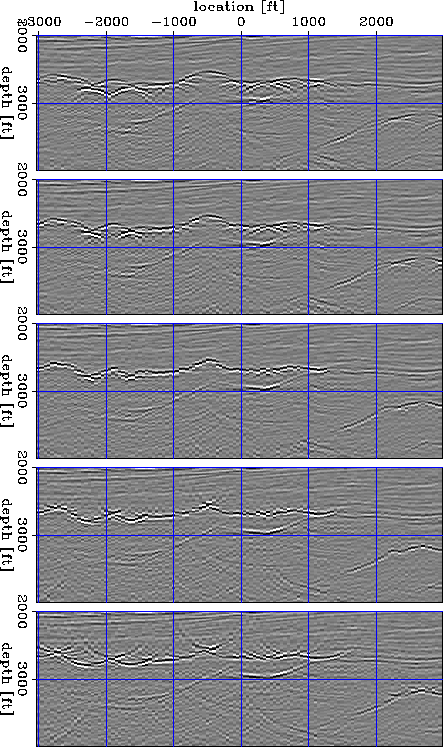
Figure 5 shows this image after residual migration with
various velocity ratios Sava (2003).
From top to bottom, the ratios are:
1.04, 1.00, 0.96, 0.92, 0.88.
At ![]() we recover the initial image.
Different parts of the image come into focus at different
values of the velocity ratio.
we recover the initial image.
Different parts of the image come into focus at different
values of the velocity ratio.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
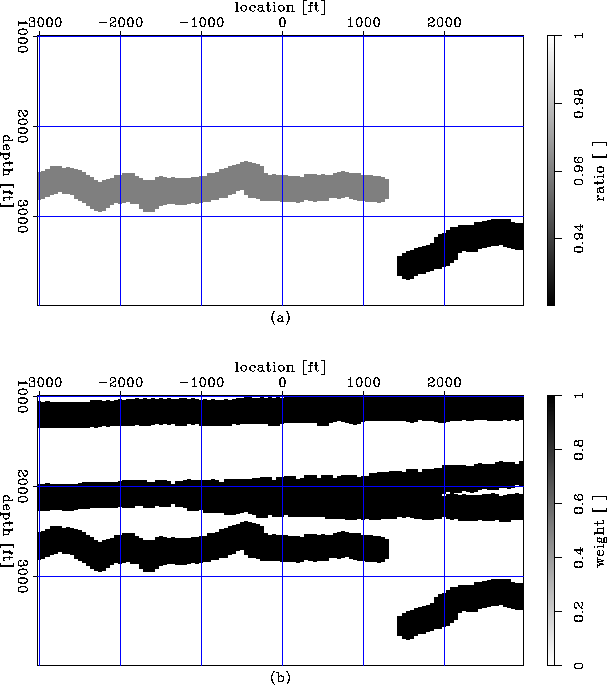
Figure 6(a) shows the picked velocity ratios at various locations
in the image. The white background corresponds to picked ![]() , and
the gray shades correspond to
, and
the gray shades correspond to ![]() between and 0.08.
Figure 6(b) shows a map of the weights (
between and 0.08.
Figure 6(b) shows a map of the weights (![]() )
associated to each picked value.
The white background corresponds to
)
associated to each picked value.
The white background corresponds to ![]() , indicating low confidence
in the picked values, and the dark regions correspond to
, indicating low confidence
in the picked values, and the dark regions correspond to ![]() , indicating
high confidence in the picked values.
In this example, we disregard
regions where we did not pick any diffractions.
All other regions receive an arbitrary
ratio value (
, indicating
high confidence in the picked values.
In this example, we disregard
regions where we did not pick any diffractions.
All other regions receive an arbitrary
ratio value (![]() ), but also a low weight such that they do not
contribute to the inversion.
Exceptions include the water bottom, for which
we assign a high weight of the picked ratio
), but also a low weight such that they do not
contribute to the inversion.
Exceptions include the water bottom, for which
we assign a high weight of the picked ratio ![]() ,and a few other reflectors for which we did not have any
diffraction focusing information.
,and a few other reflectors for which we did not have any
diffraction focusing information.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Figure 7(a) shows the slowness perturbation obtained after 20 iterations of zero-offset inversion from the image perturbation in Figure 7(b). The image perturbation is non-zero only in the regions where we had diffractions we could pick, as indicated by Figure 6. The smooth slowness perturbation is further constrained by the regularization operator we use, which is a simple Laplacian penalizing the rough portions of the model.
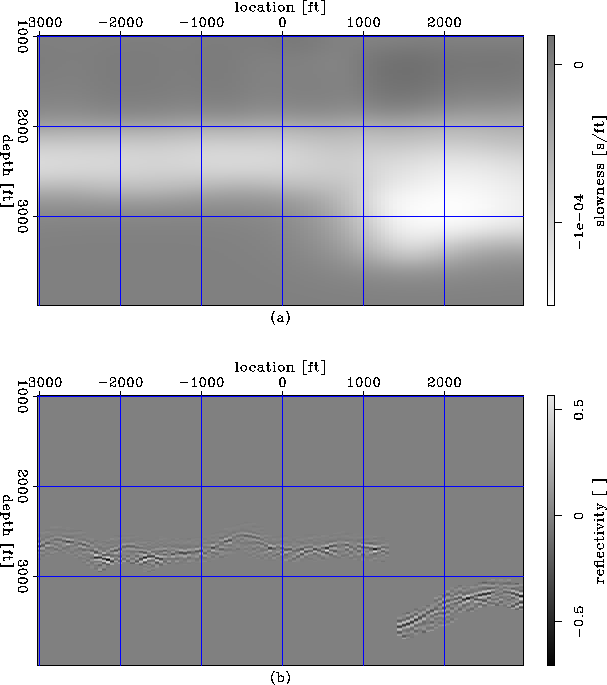 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Figure 8(a) shows the updated slowness model and Figure 8(b) shows the zero-offset migrated image corresponding to the updated model. Most of the diffractions at the top of the salt have been collapsed, and the rough top of the salt can be easily picked. The diffractions corresponding to the salt bodies at x=2000-4000 ft, z=3500 ft are not fully collapsed, indicating that another nonlinear iteration involving residual migration and picking might be necessary.
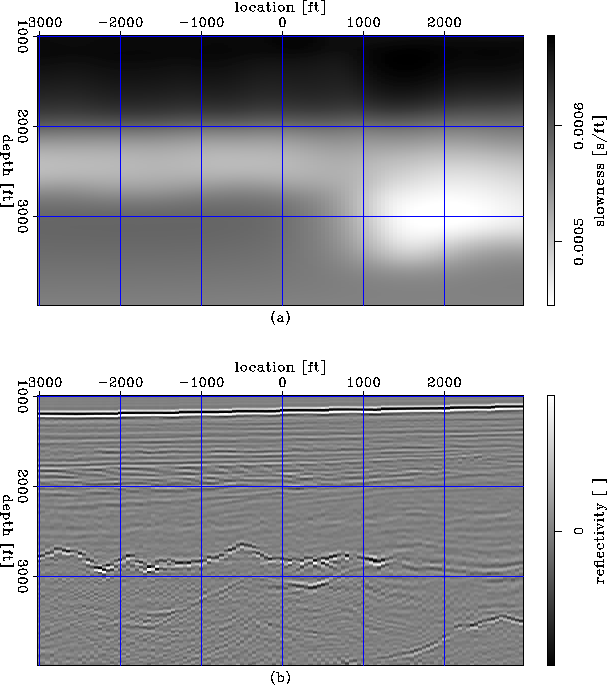 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Finally, Figure 9 shows prestack migrated images using the initial velocity model (a) and the one updated using zero-offset focusing (b). The top panels depict stacks, and the bottom panels depict angle-domain common-image gathers (ADCIG) Sava and Fomel (2003). The ADCIGs show substantial bending after migration with the initial velocity, but they are mostly flat after migration with the updated velocity, although none of the moveout information has been used for velocity update. Figure 10 shows two ADCIGs at x=-2350 ft from the images obtained with the initial velocity model (a) and the updated velocity model (b). The ADCIG in panel (a) corresponds to a notch in the top of the salt and is complicated to use for velocity analysis. However, after migration with the updated velocity model, panel (b), the ADCIG is much simpler, and the small residual moveouts can be picked for velocity updates.
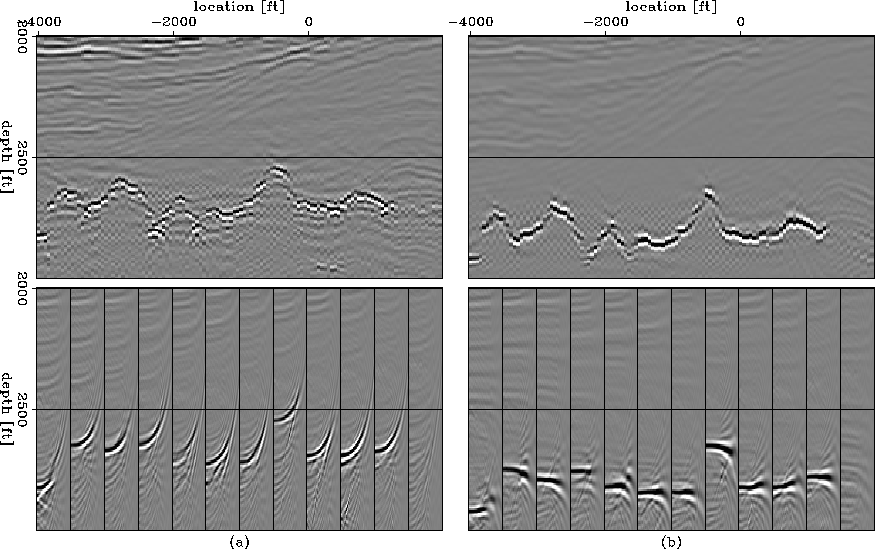 |
|
BPAITcig
Figure 10 Angle-domain common image gather obtained after migration with the initial velocity model (a) and the updated velocity model (b). |  |
A comparison of Figure 8(b) with Figure 9(b) shows a potential limitation of our technique in the presence of prismatic waves Biondi (2003). Both images are obtained with the same velocity, the first one with zero-offset data and the second one with prestack data. The imaging artifacts visible at the bottom of the deep canyons at the top of the salt in Figure 8(b) are created by prismatic waves that are not properly imaged from zero-offset data. Prismatic waves are better (though not perfectly) handled by full prestack migration, and thus the artifacts are not visible in the prestack-migrated image shown in Figure 9(b). Since these artifacts resemble uncollapsed diffractions, they may mislead the analysis of the residual migrated images and be interpreted as symptoms of velocity inaccuracies.