Examples

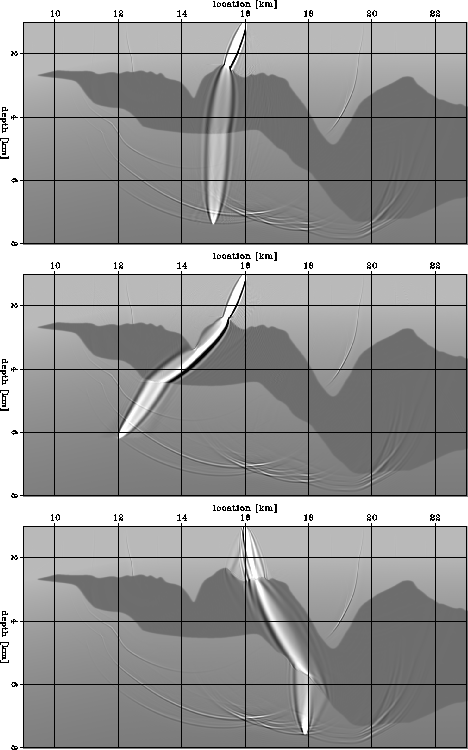
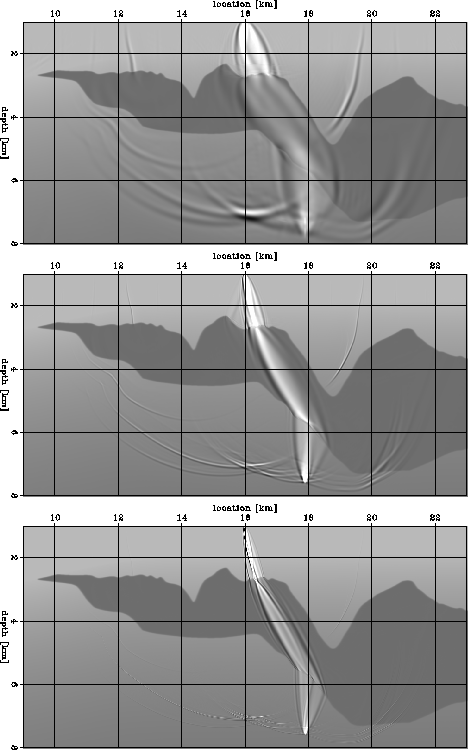
In our first example, we consider a background wavefield emerging from a fixed point source on the surface, but investigate the sensitivity kernels for various points in the image. Each panel in Figure 1 depicts a superposition of three elements: the velocity model, the band-limited wavefield corresponding to a point source on the surface, and the sensitivity kernel$\;$corresponding to a point in the subsurface.

A fundamental problem with ray-based MVA is that rays are poor approximations of the actual wavepaths when a band-limited seismic wave propagates through a rugose top of the salt. Figure 1 illustrates this issue quite clearly. It shows three sensitivity kernels for frequencies of 1-26 Hz. The top panel in Figure 1 shows a wavepath that could be reasonably approximated using the method introduced by Lomax (1994) to trace fat rays using asymptotic methods. In contrast, the wavepaths shown in both the middle and bottom panels cannot be well approximated using Lomax' method. The amplitude and shapes of these wavepaths are much more complex than a simple fattening of a geometrical ray could ever describe. The bottom panel illustrates the worst situation for ray-based tomography because the rugosity of the top of the salt has the same scale as the spatial wavelength of the seismic wave.

 

zifat
Figure 1 Kinematic sensitivity kernels for frequencies between 1 and 26 Hz for various locations in the image and a point on the surface. Each panel is an overlay of three elements: the slowness model, the wavefield corresponding to a point source on the surface at x=16 km, and wave paths (sensitivity kernels) from a point in the subsurface to the source.

 

zifrq2
Figure 2 Frequency dependence of kinematic sensitivity kernels between a location in the image and a point on the surface. Each panel is an overlay of three elements: the slowness model, the wavefield corresponding to a point source on the surface at x=16 km, and wave paths (sensitivity kernels) from a point in the subsurface to the source. The different wave paths correspond to frequency bands of 1-5 Hz (top), 1-16 Hz (middle) and 1-64 Hz (bottom). The larger the frequency band, the narrower the wave path. The end member for an infinitely wide frequency band corresponds to an infinitely thin geometrical ray.

The fundamental reason why the true wavepaths cannot be approximated using fattened geometrical rays is that they are frequency dependent. Figure 2 illustrates this dependency by depicting the wavepath shown in the bottom panel of Figure 1 as a function of the temporal bandwidth: 1-5 Hz (top), 1-16 Hz (middle), and 1-64 Hz (bottom). The width of the wavepath decreases as the frequency bandwidth increases, and the focusing and defocussing of the energy varies with the frequency bandwidth.

In the next example (Figures 3 and 4) we compare the shapes of sensitivity kernels when we change the type of source for the background wavefield, its frequency content and the method used to generate an image perturbation in the subsurface. As for the preceding example, we show the results as a superposition of the velocity model, the background wavefield and the sensitivity kernel  from a fixed point in the subsurface.

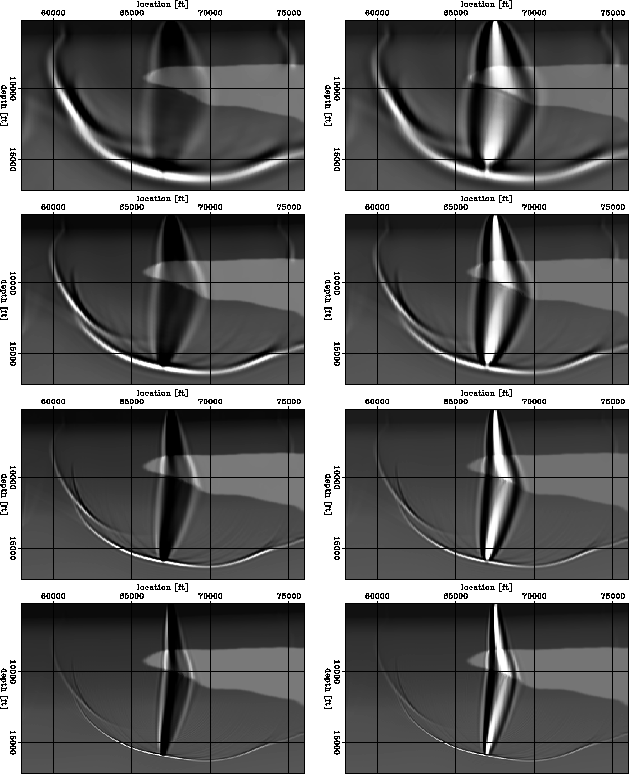
Figure 3 shows the sensitivity kernels for a point source on the surface, and Figure 4 shows the sensitivity kernels for a plane-wave propagating vertically at the surface. In both pictures, the left column corresponds to kinematic image perturbations of equation (6), and the right column corresponds to amplitude image perturbations of equation (7) obtained by scaling of the background image by an arbitrary number. From top to bottom, we show sensitivity kernels of increasing frequency range: 1-4 Hz, 1-8 Hz, 1-16 Hz and 1-32 Hz. Once again, we can see the large frequency dependence of the sensitivity kernels. The area of sensitivity reduces with increased frequency which is a clear indication that a frequency dependent migration velocity analysis method like WEMVA can better handle subsalt environments with patchy illumination and that illumination itself is a frequency dependent phenomenon which needs to be addressed in this way.

 

fat2d.Tray2a
Figure 3 The dependence of sensitivity kernels to frequency and image perturbation. From top to bottom, the frequency range is 1-4 Hz, 1-8 Hz, 1-16 Hz and 1-32 Hz. The left column corresponds to kinematic image perturbations, and the right column corresponds to dynamic image perturbations. The wavefield is produced from a point source.

 

fat2d.Tray2b
Figure 4 The dependence of sensitivity kernels to frequency and image perturbation. From top to bottom, the frequency range is 1-4 Hz, 1-8 Hz, 1-16 Hz and 1-32 Hz. The left column corresponds to kinematic image perturbations, and the right column corresponds to dynamic image perturbations. The wavefield is produced by a horizontal incident plane-wave.

Finally, we show wave-equation MVA sensitivity kernels for a 3D velocity model Figure 5 corresponding to a salt environment. We consider the case of a point source on the surface and data with a frequency range of 1-16 Hz. Figure 6 shows the sensitivity kernel  for a kinematic image perturbation, while Figure 7 for a amplitude image perturbation. In both cases, the shapes of the kernels are complicated, which is an expression of the multipathing occurring as waves propagate through rough salt bodies. The horizontal slice indicates multiple paths linking the source point on the surface with the image perturbation in the subsurface.

One noticeable characteristic is that the sensitivity kernels constructed from amplitude image perturbations show the largest sensitivity in the center of the kernel, as opposed the kinematic kernels which show the largest sensitivity away from the central path. This phenomenon was discussed by Dahlen et al. (2000) in the context of finite-frequency traveltime tomography. We illustrate it for WEMVA in Figure 8 with two horizontal slices in the sensitivity kernels shown in Figures 6 and 7.

 

fat3.sC
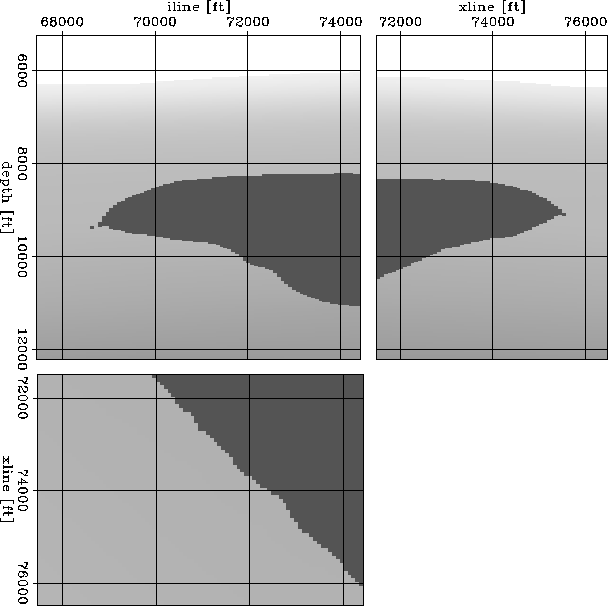
Figure 5 3D slowness model.

 

fat3.fp3
Figure 6 3D sensitivity kernels for wave-equation MVA. The frequency range is 1-16 Hz. The kernels are complicated by the multipathing occurring as waves propagate through the rough salt body. The image perturbation corresponds to a kinematic shift.

 

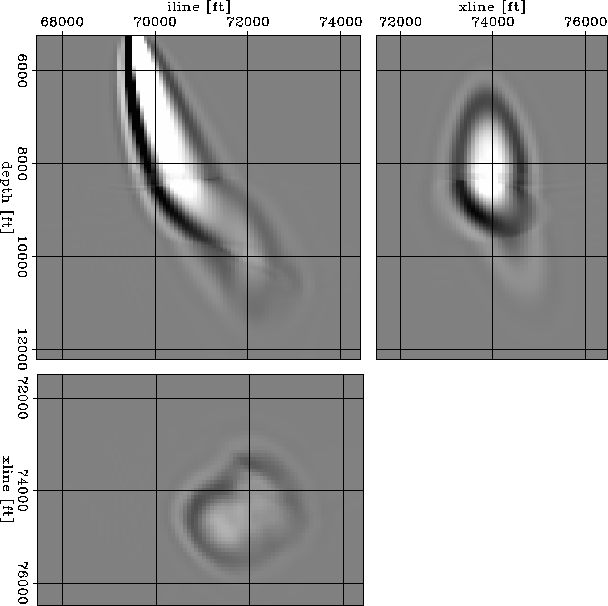
fat3.fq3
Figure 7 3D sensitivity kernels for wave-equation MVA. The frequency range is 1-16 Hz. The kernels are complicated by the multipathing occurring as waves propagate through the rough salt body. The image perturbation corresponds to an amplitude scaling.

 

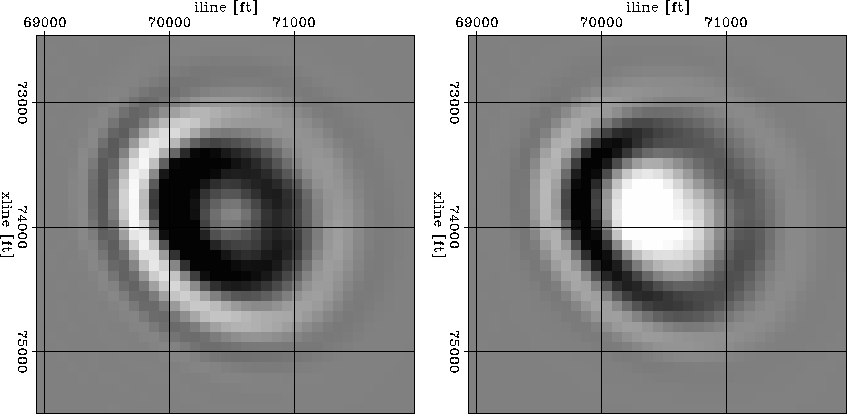
fat3.svty
Figure 8 Cross-section of 3D sensitivity kernels for wave-equation MVA. The left panel corresponds to an image perturbation produced a kinematic shift, while the right panel corresponds to an image perturbation produced by amplitude scaling. The lowest sensitivity occurs in the center of the kinematic kernel (left). In contrast, the maximum sensitivity occurs in the center of the kernel (right).