Application to propagation in a more general v(x,z) model

The velocity model used by Vlad et al. (2003) for examining the effects of the amplitude corrections was particularly unsuitable for the problem. It belonged actually to a limit case in which the amplitude corrections canceled themselves. We will show below why that was the case and we will analyze the effects of the corrections by picking amplitudes at each midpoint in a wavefield depth slice.

At each downward continuation step, the propagation amplitude correction applied to the wavefield is:  

$$P'_z = P_z e^{-\frac{v_z\Delta z}{2v\left(x,z\right)} \frac{1}{1-\left[\frac{v\left(x,z\right)k_x}{\omega}\right]^2} },$$ (1)

where v_z denotes the vertical gradient of the velocity. When variations of velocity in the x direction exist, this exponential is strictly noncommutative with the downward continuation step. The noncommutativity however becomes weak in the particular case when the laterally varying velocity is symmetrical with respect to a horizontal plane. In the case of such symmetry, corrections of the same magnitude along midpoint, but of different sign (because of an opposing sign for v_z) cancel each other. The corrections in the lower half of the velocity model in Figure 3 of Vlad et al. (2003) were therefore erasing the effects of the ones performed in the upper half. As a result, Figure 4 of Vlad et al. (2003) was not showing any results of the correction.

Recognizing that such a symmetrical configuration is not very plausible geologically, we downward continued (with split-step) only through the upper half of the respective velocity model. This half is depicted in Figure 1.

 

g1
Figure 1 Top panel: Upper half of the velocity model used by Vlad et al. (2003). Figure 2 shows the amplitudes produced by propagation through this velocity model. Bottom panel: Rays shot from (0,0), shown for an enhancement of the intuitive appreciation of the focusing during the propagation.

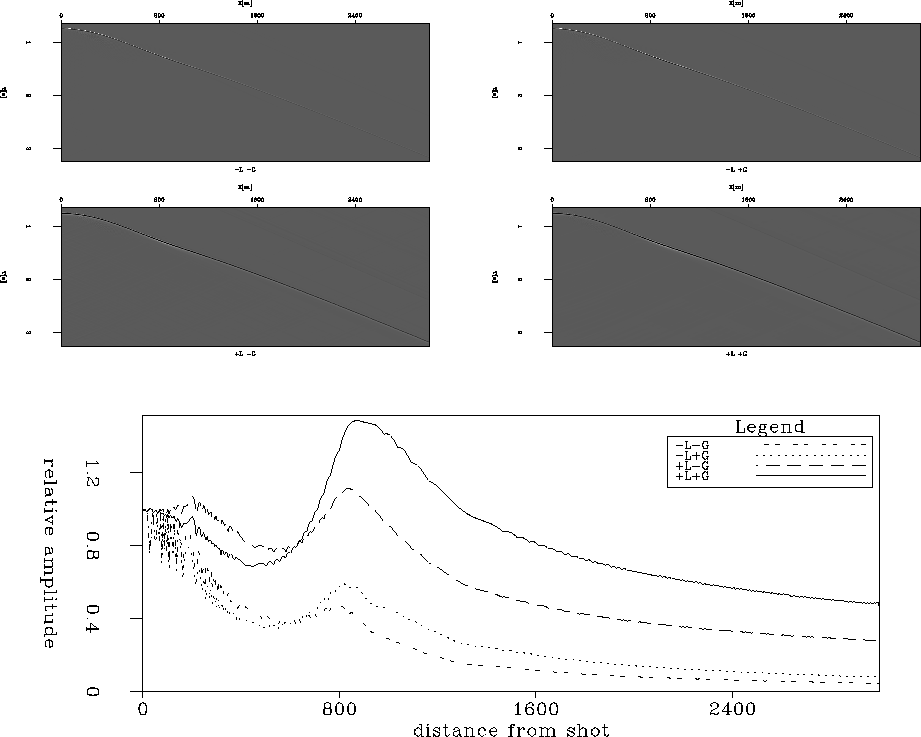
The top panels in Figure 2 show the wavefield at a depth of 1000m. The four panels represent all the combinations of applying (``+'') or not (``-'') the boundary condition correction (``L'') and/or the propagation correction (``G''). The lower half of the figure shows the maximum amplitudes picked for each midpoint. The effect of the propagation correction (Curves ``-L+G'' and ``+L+G'') is visible now as increased focusing and reduced amplitude decay with offset. The boundary condition correction (Curves ``+L-G'' and ``+L+G'') also has a strong effect; it especially diminishes the amplitude decay. We expect the two Zhang corrections to increase, when cummulated, power for large dips and for large incidence angles on the reflector.

 

g2
Figure 2 ``L'' denotes the boundary condition correction, ``G'' denotes the propagation correction, a "+'' shows that the respective correction was applied, and a ``-'' shows that it was not. Top panels: Wavefield generated by a shot at (0,0) in the velocity model from Figure 1, and recorded at the bottom of that velocity model. Bottom panel: Maximum amplitudes picked for each x location in the top panels.