




Next: Application of the CGG
Up: Conjugate Guided Gradient(CGG) method
Previous: CGG with iteratively reweighted
In the previous two subsections, we examined the meaning the of weighting
the residual and the gradient vector, respectively.
Since applying the weighting in both residual space
and model space is nothing but changing the direction of the descent
for the solution search,
the weighting is not limited either to residual or to model space.
We can weight both the residual and the gradient,
 iterate {
iterate {
![$\bold W_r \quad\longleftarrow\quad{\bf diag}[f(\bold r)]$](img43.gif)
![$\bold W_m \quad\longleftarrow\quad{\bf diag}[f(\bold m)]$](img44.gif)
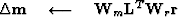
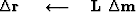
 } .
} .
Again, the above CGG algorithm is different from the conventional CG method
only in the step of gradient computation.
Whether we modify the gradient in the residual sense
or in the model sense,
it changes only the gradient direction,
or the direction in which the solution is sought.
Therefore the CGG algorithm always converges to a solution.





Next: Application of the CGG
Up: Conjugate Guided Gradient(CGG) method
Previous: CGG with iteratively reweighted
Stanford Exploration Project
5/23/2004
iterate {
![$\bold W_r \quad\longleftarrow\quad{\bf diag}[f(\bold r)]$](img43.gif)
![$\bold W_m \quad\longleftarrow\quad{\bf diag}[f(\bold m)]$](img44.gif)
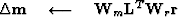
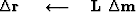
} .