




Next: The imaging condition
Up: Theory
Previous: Scalar Wave Equation for
Assuming applicability of the scalar wave equation given by
equation (1), the first step in GPR shot-profile
migration is the extrapolation of surface-recorded data to depth.
This is done by applying a one-way wave-equation operator to an
arbitrary wavefield, as a function of space and frequency, to yield
the wavefield at a deeper level:
| 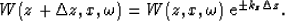 |
(3) |
Here, the positive or negative exponent corresponds to causal or
acausal propagation, respectively, and 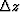 is the size of the
downward continuation step. The vertical wavenumber, kz, is
calculated from the scalar wave-equation dispersion relation,
is the size of the
downward continuation step. The vertical wavenumber, kz, is
calculated from the scalar wave-equation dispersion relation,
| 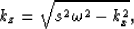 |
(4) |
where kx is the horizontal Fourier wavenumber component of the data
wavefield.
Surface-recorded wavefields are extrapolated to all depths within the
model through successive applications of equation (3)
using a vertical wave-number given by equation (4).
Although equation (4) is strictly valid only for vertically
stratified media, techniques exist to extend it to laterally varying
media. We employ a split-step Fourier approach Stoffa et al. (1990) that involves
approximating kz in equation (4) using a Taylor series
expansion about a reference slowness, s0:
| 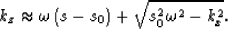 |
(5) |
The first, mixed-domain term in equation (5) acts as a
local correction to the second term that handles the bulk of the
propagation. Increased accuracy can be achieved by summing the
results of multiple reference velocity steps in order to minimize the
quantity s(x)- s0.
Shot-profile migration directly mimics the data collection process by
migrating individual shot records. Receiver wavefields are comprised
of individual shot profiles and are propagated acausally. Source
wavefields have the same geometry, but are initially zero except for
an appropriate source function at the transmitter location, and are
propagated causally.





Next: The imaging condition
Up: Theory
Previous: Scalar Wave Equation for
Stanford Exploration Project
5/23/2004