




Next: The chicken and the
Up: Theory
Previous: Phase-rayfields
Wavefield extrapolation in ray-coordinates requires casting the
acoustic wave-equation not in the usual Cartesian representation, but
rather in a system parameterized by phase-ray variables.
In 2-D, these variables consist of  , the one-way travel time
from a source/receiver point along the direction of a ray, and
, the one-way travel time
from a source/receiver point along the direction of a ray, and 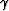 ,the direction across the rayfront at a constant time step.
A cartoon illustrating ray-coordinate geometry is presented in
Figure 1.
,the direction across the rayfront at a constant time step.
A cartoon illustrating ray-coordinate geometry is presented in
Figure 1.
raycoord
Figure 1 Cartoon illustrating the phase-ray
coordinate system and its relation to the Cartesian basis. Variable
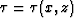 is the direction along a single ray, and parameter is the direction along a single ray, and parameter
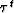 is an isochron or rayfront. Variable is an isochron or rayfront. Variable 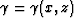 is
the coordinate across the rayfront at a constant is
the coordinate across the rayfront at a constant  step, and
parameter step, and
parameter 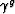 is a ray. Grey lines illustrate the mapping
between ray point is a ray. Grey lines illustrate the mapping
between ray point 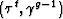 and Cartesian point (xo,zo).
Angle and Cartesian point (xo,zo).
Angle 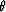 is a rotation angle between the ray and the z-axis
(assumed to be positive downward). is a rotation angle between the ray and the z-axis
(assumed to be positive downward).
|
|  |

Note that the dimensions of time and space coordinates  and
and 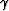 are seconds and meters, respectively.
are seconds and meters, respectively.
The 2-D acoustic wave-equation for wavefield, 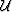 , at frequency,
, at frequency,
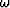 , in ray-coordinates is Sava and Fomel (2003),
, in ray-coordinates is Sava and Fomel (2003),
| ![\begin{displaymath}
\frac{1}{v J} \left[ \frac{\partial}{\partial\t} \left( \fra...
...partial\gamma} \right) \right]= -\frac{\omega^2}{v^2} {\cal U},\end{displaymath}](img27.gif) |
(6) |
where v is the velocity function, and J is the ray-coordinate
Jacobian or geometrical ray spreading factor given by,
| ![\begin{displaymath}
J=\left[ \frac{\partial x_k}{\partial\gamma} \frac{\partial x_k}{\partial\gamma} \right]^
{\frac{1}{2}}.\end{displaymath}](img28.gif) |
(7) |
Importantly, parameter J is solely a component of ray-coordinates
and is independent of wavefield extrapolated on the coordinate system.
Analogous to wave-equation extrapolation in Cartesian coordinates, a
dispersion relation must be specified that forms the basis for all
derived ray-coordinate extrapolation operators. The relation
being sought is the wavenumber along the ray direction, 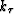 .Following Sava and Fomel (2003),
the partial derivative operators in equation (6) are
expanded out to generate a second-order partial differential equation
with non-zero cross derivatives. Fourier-domain wavenumbers are then
substituted for the partial differential operators acting on
wavefield,
.Following Sava and Fomel (2003),
the partial derivative operators in equation (6) are
expanded out to generate a second-order partial differential equation
with non-zero cross derivatives. Fourier-domain wavenumbers are then
substituted for the partial differential operators acting on
wavefield, 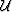 , and the quadratic formula is applied to yield the
expression for
, and the quadratic formula is applied to yield the
expression for 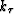 ,
,
| ![\begin{displaymath}
k_\tau= \frac{{\rm i}v}{2 J} \frac{\partial}{\partial \tau}\...
...t) k_\gamma-
\frac{v^2}{J^2} k_\gamma^2 \right]^{\frac{1}{2}}.\end{displaymath}](img30.gif) |
(8) |
Note, again, that quantity 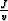 depends solely on the
coordinate system and is independent of the wavefield being
propagated.
depends solely on the
coordinate system and is independent of the wavefield being
propagated.
One relatively straightforward manner to apply wavenumber 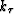 in an extrapolation scheme is to develop the ray-coordinate equivalent
of Claerbout's classic 15 equation Claerbout (1985). This
involves a second-order Taylor series expansion of the radical in
equation (8), and the identification of Fourier dual
parameters
in an extrapolation scheme is to develop the ray-coordinate equivalent
of Claerbout's classic 15 equation Claerbout (1985). This
involves a second-order Taylor series expansion of the radical in
equation (8), and the identification of Fourier dual
parameters 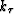 and
and 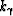 with their space domain derivative
counterparts
with their space domain derivative
counterparts 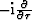 and
and 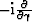 .
The ray-coordinate formula corresponding to the 15equation is,
.
The ray-coordinate formula corresponding to the 15equation is,
| ![\begin{eqnarray}
\frac{\partial{\cal U}}{\partial\t} \approx
&-& \frac{v}{2J}\fr...
...c{v^2}{J^2} \right]
\frac{\partial^2 {\cal U}}{\partial \gamma^2},\end{eqnarray}](img36.gif) |
|
| (9) |
where 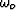 may be considered as the effective (non-stationary)
frequency,
may be considered as the effective (non-stationary)
frequency,
| ![\begin{displaymath}
\omega_o = \omega\left[ 1 - \left( \frac{v}{2 \omega J} \fra...
...tau}\left( \frac{J}{v}\right)
\right)^2 \right]^{\frac{1}{2}}.\end{displaymath}](img38.gif) |
(10) |
Equation (9) may be solved in 2-D using fully implicit finite
difference methods (e.g. Crank-Nicolson) and fast tridiagonal solvers.
After wavefield solution, 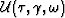 , has been computed at all
rayfield locations, the result is mapped to Cartesian coordinates
using sinc-based interpolation operators in a neighborhood about
each mapped point.
, has been computed at all
rayfield locations, the result is mapped to Cartesian coordinates
using sinc-based interpolation operators in a neighborhood about
each mapped point.





Next: The chicken and the
Up: Theory
Previous: Phase-rayfields
Stanford Exploration Project
5/23/2004


![]() and
and ![]() are seconds and meters, respectively.
are seconds and meters, respectively.
![]() , at frequency,
, at frequency,
![]() , in ray-coordinates is Sava and Fomel (2003),
, in ray-coordinates is Sava and Fomel (2003),
![]() .Following Sava and Fomel (2003),
the partial derivative operators in equation (6) are
expanded out to generate a second-order partial differential equation
with non-zero cross derivatives. Fourier-domain wavenumbers are then
substituted for the partial differential operators acting on
wavefield,
.Following Sava and Fomel (2003),
the partial derivative operators in equation (6) are
expanded out to generate a second-order partial differential equation
with non-zero cross derivatives. Fourier-domain wavenumbers are then
substituted for the partial differential operators acting on
wavefield, ![]() , and the quadratic formula is applied to yield the
expression for
, and the quadratic formula is applied to yield the
expression for ![]() ,
,
![\begin{displaymath}
k_\tau= \frac{{\rm i}v}{2 J} \frac{\partial}{\partial \tau}\...
...t) k_\gamma-
\frac{v^2}{J^2} k_\gamma^2 \right]^{\frac{1}{2}}.\end{displaymath}](img30.gif)
![]() in an extrapolation scheme is to develop the ray-coordinate equivalent
of Claerbout's classic 15 equation Claerbout (1985). This
involves a second-order Taylor series expansion of the radical in
equation (8), and the identification of Fourier dual
parameters
in an extrapolation scheme is to develop the ray-coordinate equivalent
of Claerbout's classic 15 equation Claerbout (1985). This
involves a second-order Taylor series expansion of the radical in
equation (8), and the identification of Fourier dual
parameters ![]() and
and ![]() with their space domain derivative
counterparts
with their space domain derivative
counterparts ![]() and
and ![]() .
The ray-coordinate formula corresponding to the 15equation is,
.
The ray-coordinate formula corresponding to the 15equation is,
![\begin{eqnarray}
\frac{\partial{\cal U}}{\partial\t} \approx
&-& \frac{v}{2J}\fr...
...c{v^2}{J^2} \right]
\frac{\partial^2 {\cal U}}{\partial \gamma^2},\end{eqnarray}](img36.gif)
![\begin{displaymath}
\omega_o = \omega\left[ 1 - \left( \frac{v}{2 \omega J} \fra...
...tau}\left( \frac{J}{v}\right)
\right)^2 \right]^{\frac{1}{2}}.\end{displaymath}](img38.gif)