




Next: Synthetic Testing
Up: Wilson et al.: Teleseismic
Previous: Source-Receiver Geometry of Teleseismic
The primary advantage of the shot-profile formulation of wave
equation migration for teleseismic imaging comes from
the ability to separate the source and receiver wavefields for
independent propagation during propagation. Shot-profile
migration separates the total wavefield into
source and receiver wavefields that are each propagated separately (by
Fourier-domain multiplication) with the appropriate single square root (SSR) operators Claerbout (1995).
| 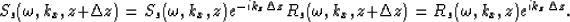 |
(1) |
Here Ss is the source wavefield for a recorded teleseismic event s and Rs represents the
receiver wavefield. The negative sign on the single square root
operator exponent applied to the source wavefield denotes an
initially downgoing wavefield.
To represent source and receiver wavefields traveling in the same
(upgoing) direction we apply a positive exponent to the single square
root operator of each wavefield. The strength of this method comes from the implicit assignment of source and receiver wavefield mode (P or S waves) and propagation direction based on the choice of velocity model and operator exponent, respectively. Following the passive seismic methodology developed previously by Claerbout (1968), we attempt to exploit this direct observation of the source wavefield thereby minimizing the amount of prior assumptions and preprocessing Artman and Shragge (2003). Single components of our recorded wavefield may be treated as a source representation with the particular component chosen according to the scattering mode of interest. Table 1 shows the sign and velocity model used to propagate both the source and receiver wavefields for several possible scattering modes.
Table 1:
Table listing of the scattering modes, propagation velocity, and propagaton direction for each source and receiver wavefield for different scattering modes.
| Mode |
Scattering Mode |
Source Prop. Dir. |
S. Velocity |
R. Velocity |
Rec. Component |
| 1 |
FS P-P |
- |
P |
P |
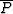 |
| 2 |
FS P-S |
- |
P |
S |
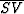 |
| 3 |
BS P-P |
+ |
P |
P |
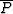 |
| 4 |
BS P-S |
+ |
P |
S |
 |
| 5 |
BS S-P |
+ |
S |
P |
 |
| 6 |
BS S-S |
+ |
S |
S |
 |
| 7 |
BS S-S |
+ |
S |
S |
 |
After propagation of the wavefields, image computation results from a frequency summation of the deconvolution at each depth.
| 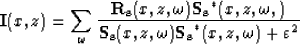 |
(2) |
After computing individual images from each scattering mode for individual earthquakes, we create composite images for each scattering mode by summing images from all recorded earthquakes. We produce a final image by summing all images produced by all scattering modes.





Next: Synthetic Testing
Up: Wilson et al.: Teleseismic
Previous: Source-Receiver Geometry of Teleseismic
Stanford Exploration Project
5/23/2004