Direct migration of white-noise data

$\begin{multline} R^+\left(\boldsymbol{x}_A , \boldsymbol{x}_B , \omega \right) +... ...\{ T^-_{obs}\left(\boldsymbol{x}_B , \omega \right)\right\}^* \; .\end{multline}$

Above, $R^+\left(\boldsymbol{x}_A , \boldsymbol{x}_B , \omega \right)$ is the reflection response measured at point x_A at the surface ( $\partial {\cal D}_0$ ) in the presence of an impulsive source at x_B, while $T^-_{obs}\left(\boldsymbol{x}_A , \omega \right)$ is the transmission response measured at the surface point x_A in the presence of noise sources in the subsurface. Downward extrapolaton of $R^+\left(\boldsymbol{x}_A , \boldsymbol{x}_B , \omega \right)$ to common surface locations $\xi_A, \xi_B$ at an arbitrarily greater depth is described by

$\begin{multline} R^+\left(\boldsymbol{\xi}_A , \boldsymbol{\xi}_B , \omega \righ... ... \omega \right)\right\}^* d\boldsymbol{x}_A d\boldsymbol{x}_B \; ,\end{multline}$

where $R^+\left(\boldsymbol{\xi}_A , \boldsymbol{\xi}_B , \omega \right)$ is the reflection response extrapolated from the surface to some subsurface level and $W^+\left(\boldsymbol{\xi}_A , \boldsymbol{x}_A , \omega\right)$ and $W^-\left(\boldsymbol{x}_B , \boldsymbol{\xi}_B , \omega \right)$ are forward-extrapolation operators. If we substitute equation (

) into equation (

) we obtain

$\begin{multline} R^+\left(\boldsymbol{\xi}_A , \boldsymbol{\xi}_B , \omega \righ... ...oldsymbol{x}_B \right\}^* \\ + \; \text{anti-causal terms} \; . \end{multline}$

In the above relation, we used the fact that the reflection coefficient of the free-surface is r=-1 and the reciprocity relation of the forward-extrapolation operator $W^-\left(\boldsymbol{x}_B , \boldsymbol{\xi}_B , \omega \right)=W^+\left(\boldsymbol{\xi}_B , \boldsymbol{x}_B , \omega \right)$ . Equation (

) shows that by inverse-extrapolating the transmission response $T_{obs}^-\left(\boldsymbol{x}_A , \omega \right)$ at all $\boldsymbol{x}_A$ at the surface to a certain subsurface level, and forward-extrapolating the downward-reflected transmission response $rT_{obs}^-\left(\boldsymbol{x}_B , \omega \right)$ at all $\boldsymbol{x}_B$ to the same subsurface level, followed by cross-correlation of the resultant wave fields, we obtain the downward extrapolated reflection response. If we subsequently apply the imaging condition, we can image the subsurface at that level Armtan et al. (2004)). If we compare this process with shot-profile migration Claerbout (1971) we can see that they are identical. This means that based on shot-profile migration we can directly migrate passive white-noise data without the need to first simulate the reflection shot gathers.

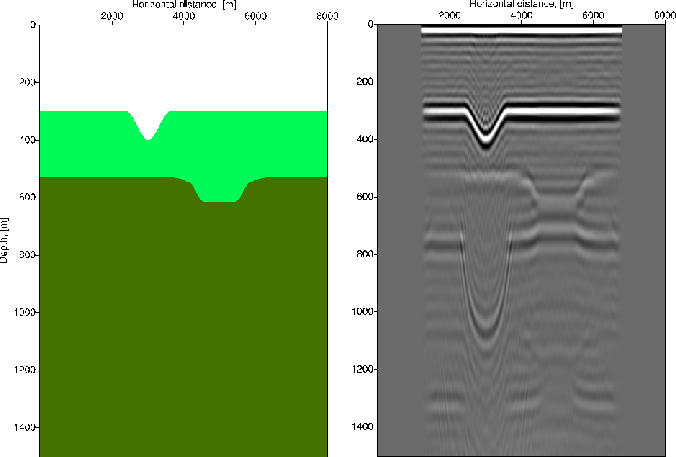
As Figure 1 shows, we may thus use two paths for obtaining a migrated image from passive data. Following the first path, we first cross-correlate the transmission responses recorded at the surface to simulate reflection shot gathers, then we extrapolate the simulated shot gathers and apply the imaging condition (this process was also proposed by Schuster 2001 and named Interferometric Imaging). The other way is to directly migrate the passive data - first we extrapolate the transmission responses recorded at the surface to some subsurface level, then we cross-correlate them and apply the imaging condition. The left panel of Figure 2 shows a double syncline model used to generate transmission responses of white-noise sources in the subsurface. These transmissions were afterwards migrated using both migration methods described above. The results were identical (Figure 2 ).

**Figure 1:** Two paths can be followed to obtain a migrated image from passive data.
$\begin{figure} \begin{center} \begin{tabular} {ccccc} \fbox {$T_{obs}^-\left(\b... ..._A , \boldsymbol{\xi}_B , \omega \right)$} \end{tabular}\end{center}\end{figure}$