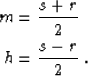Next: Flat earth synthetic
Up: Artman et al.: Aliasing
Previous: Introduction
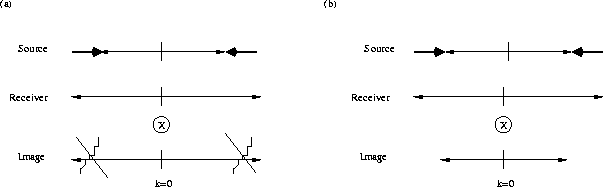
The standard seismic acquisition grid is presented in panel (a) of
Figure 1. Ease of drafting and understanding
conventionally has lead geophysicists to draw these axes 90o to
each other. However, there is no reason to do so. Further, imposing
the intuition that these axes are mathematically orthogonal leads to
difficulties in interpreting Fourier sampling criteria that we aim to
investigate here. These axes inhabit the same physical space along a
2D seismic acquisition line. Plotting them orthogonally
casts an inappropriate feeling of a second physical dimension.
nybox
Figure 1 (a) The
standard representation of the seismic acquisition grid. (b) Viable
alternative to conventional orthogonal drawings. (c) Fourier
transform of (a) with Nyquist sampling limits included. (d) Fourier
transform of (b) with Nyquist sampling limits included.
|
| 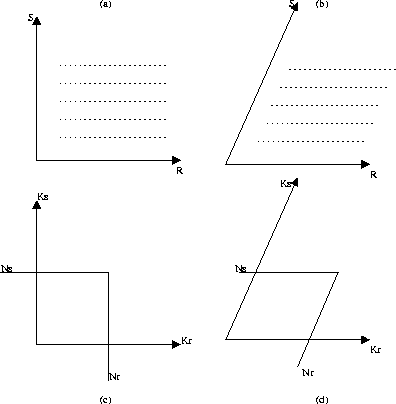 |

At the limit of this argument, we contend that it is much easier to
de-couple completely the origins of these axis and plot them parallel
to each other. Having performed a Fourier transform across space of
both the source and receiver axes, we present them in Figure
2.
waveline
Figure 2 Lengths of the
source, receiver and image axes in the Fourier domain. The
circle with an x indicates the multiplication of the data
axes to produce the image surface location axis during the
imaging condition. Aliased replications from the source axis
are represented by the bold lines pointing toward the origin. (a)
If the image spaced is sampled as finely as the receiver axis,
alias contamination will enter into the image. (b) Aliased
contamination from the subsampled source axes is avoided when the
two fields are compared during the imaging condition.

Viewing these three distinct axes separately aids in the
interpretation of this entire argument. Unfortunately, there is an
historic tendency when analyzing the acquisition grid coordinates to
include midpoint-offset, mh, axes as diagonal axes to those shown in
Figure 1. We will avoid the use of midpoint while
casting this presentation largely in the terms of shot-profile
migration, as well as explain later the development of our x-axis
during the imaging condition. Further, when they are superposed, an
incorrect stretching is implied. We will briefly consider the mid-point
axis, in order to highlight the danger of this practice.
The mapping transformation of energy from one coordinate frame to the
other has been historically defined as:
| 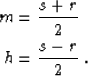 |
(1) |
| (2) |
The Jacobian of this system is thus,
| 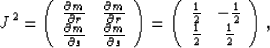 |
(3) |
which makes the determinant 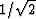 . Drawing a midpoint axis
along the 45o line of the sr-axis is confusing when someone
attempts to find value of a particular midpoint location on the
plane. Some measurement of distance must be employed as a zero-offset
location does not lie on one of the original axes. The next problem
we then face is which of the multitude of distance measures we should
select: l?. The historic choice has been the square-root of the
sum of the squares: l2. If we make that choice, we then apply the
determinant presented above to cancel the
. Drawing a midpoint axis
along the 45o line of the sr-axis is confusing when someone
attempts to find value of a particular midpoint location on the
plane. Some measurement of distance must be employed as a zero-offset
location does not lie on one of the original axes. The next problem
we then face is which of the multitude of distance measures we should
select: l?. The historic choice has been the square-root of the
sum of the squares: l2. If we make that choice, we then apply the
determinant presented above to cancel the 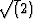 factor associated
with the norm that so naturally lends itself to pieces of paper. We
could have chosen any norm. Each of them would return a different
number, and none of them have any more or less value for locating
a seismic image on the surface of the earth.
factor associated
with the norm that so naturally lends itself to pieces of paper. We
could have chosen any norm. Each of them would return a different
number, and none of them have any more or less value for locating
a seismic image on the surface of the earth.
The cross-correlation imaging condition with subsurface offset
Rickett and Sava (2001)
| 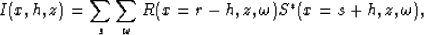 |
(4) |
combines the two independently propagated wavefields, Source and
Receiver ,and generates the surface location axis x with the
relationship within the arguments of the two wavefields. Note that
these relations are equations for a line where both the source
coordinate, s, and receiver coordinate, r, coexist. Here we see
the distinction between the surface location coordinate x and
midpoint. The x-axis fallows directly from the mathematics of
migration. With the multiplication (across space) associated with the
correlation (along time) of equation (4), the cartoons
in Figure 2 should be recalled.
The Appendix develops in rigorous detail the wavenumber limits
acceptable in the image to eliminate completely alias contamination. The
analysis of the problem centers around the effects of the
migration process on the data grid, without needing to consider the
values of the data on each grid node. We thus draw
an analogy to the body of work available from crystallography,
where structure can be analyzed mathematically without
need to know what atom resides at any particular location.
Thankfully, the regular Cartesian grid on which we normally acquire
and process seismic data is a simple rectilinear crystal,
though of several more dimensions than seen under a microscope.
The reference crystal we will consider will be the archetypal seismic
grid where sources and receivers occupy all locations and share the
same spacing increment. The suspicious or simply inquisitive reader
can now turn to the appendix to work through the details of the
following result. The maximum allowable wavenumbers, 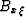 , to
avoid artifacts due to migration operator aliasing is
, to
avoid artifacts due to migration operator aliasing is
| 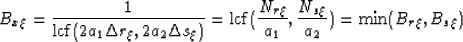 |
(5) |
where 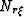 and
and 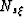 are the Nyquist frequencies defined by
fundamental sampling intervals
are the Nyquist frequencies defined by
fundamental sampling intervals 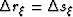 , a's are subsampling
factors, and
, a's are subsampling
factors, and 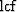 stands for least common factor (which will
change to
stands for least common factor (which will
change to 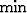 if the subsampling factors are integers. The
subscript
if the subsampling factors are integers. The
subscript 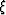 denotes the sampling associated with the model space
and is included to maintain parallelism with the appendix.
denotes the sampling associated with the model space
and is included to maintain parallelism with the appendix.
We consider three approaches to remove the aliasing
problems associated with the acquisition and subsampling situations
mentioned above during shot-profile migration. First, wavenumbers
from the source and receiver wavefields at each depth level are
band-limited to prevent the entry of aliased duplications
into the image during the imaging condition. This does not require
eliminating these components from the propagating wavefields, as we
can save appropriate portions of the wavefields in temporary buffers
for imaging condition evaluation. Second, a band-limited source
function, with a wavenumber spectrum limited to the cutoff frequencies
imposed by the resampled shot axis, is propagated throughout the
migration process. This effectively zeros energy in the aliased band
during the convolution in the imaging condition. No additional
computational overhead is required for the latter alternative, though
anti-aliasing by band-limited imaging requires two additional Fourier
transforms for a split-step Fourier migration strategy. It should be
noted, however, that both of these approaches will remove energy across
both kx and kh axes.
A third alternative is to restrict the wavenumbers of the subsurface
offset axis kh during imaging. Casting the imaging condition in
terms of it Fourier dual can allow similar mitigation options.
Because ks-kr=kh, we can select (ks,kr) combinations during
the imaging condition that do not exceed our prescribed bandwidth.
The multiplication of the source and receiver wavefields shown above
takes the form of a convolution in the Fourier domain, which can be
utilized to insert our anti-aliasing criteria. Lastly,
decimating the receiver wavefield to match the shot increment, will be
discussed in more detail with reference to shot-geophone style migration.





Next: Flat earth synthetic
Up: Artman et al.: Aliasing
Previous: Introduction
Stanford Exploration Project
5/23/2004