




Next: CONCLUSION
Up: R. Clapp: Velocity uncertainty
Previous: Limitations
To test the methodology, I started with a fairly complex 2-D synthetic.
The synthetic, shown in Figure 1, contains a realistic
reservoir bounded by a faulted anticline and a basement rock. The velocity
generally follows structure but with some low spatial frequency anomalies that
range up to 5% of the background velocity. The synthetic reservoir
is based on a real North Sea reservoir. The velocity and density
structures vary significantly within the reservoir.
The overburden was designed to break
most conventional model characterization schemes. A layer-based approach
would have difficulty with the anomalies and a gridded approach would find
the sharp contrasts introduced by the faulting troublesome.
correct
Figure 1 A 2-D synthetic. A realistic
reservoir bounded by a faulted anticline and a basement rock. The left
panel shows the velocity, the panel is the result of migrating with the correct
velocity.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

As an initial velocity estimate, I smoothed significantly the correct model.
Figure 2 shows the initial velocity and the resulting
migration. The basement reflectors are no longer flat and the anticline
structure is more compressed in shape. The common reflection point
gathers, five of which are shown in Figure 3, show significant move-out.
initial
Figure 2 The left panel shows the initial
velocity model. The right panel shows the resulting of migrating with
this velocity model.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 gathers
gathers
Figure 3 Five CRP gathers (X=2,4,6,8,10) using the velocity shown in
the left panel of Figure 2.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

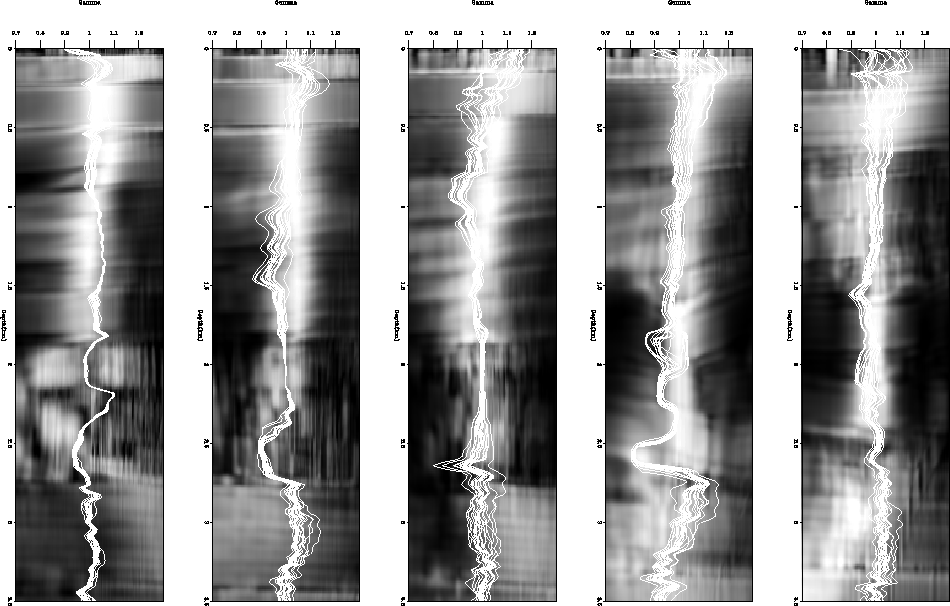
I then performed SRM semblance analysis on the dataset using 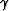 ranging from
.7 to 1.3. Figure 4 shows the semblance
scans for the same five locations as in
Figure 3.
I used the initial migration image to construct a steering filter
for the colored random number generation.
Figure 5 shows nine realizations
of applying fitting goals (12). Note how the generated random
numbers follow the image structure shown in Figure 2, but
vary dramatically from realization to realization.
I converted these random numbers to
ranging from
.7 to 1.3. Figure 4 shows the semblance
scans for the same five locations as in
Figure 3.
I used the initial migration image to construct a steering filter
for the colored random number generation.
Figure 5 shows nine realizations
of applying fitting goals (12). Note how the generated random
numbers follow the image structure shown in Figure 2, but
vary dramatically from realization to realization.
I converted these random numbers to 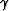 values using cdfs generated
at every location using equation (11). Thirty
realizations of
values using cdfs generated
at every location using equation (11). Thirty
realizations of 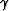 values overlay the semblance scans
in Figure 4.
The various realizations are smooth as function of depth, which is reasonable.
The amount of variance also seems reasonable. Note how when we
have a sharp semblance maximum we see almost no variation, while
when our blob is more spread out, the selected gamma values are
more diverse. Note the fourth from the left gather at
1.8 seconds. Two different maxima are present in the semblance
gather and we see that both are picked by various realizations.
Figure 6 shows nine gamma maps as a function
of space. The
values overlay the semblance scans
in Figure 4.
The various realizations are smooth as function of depth, which is reasonable.
The amount of variance also seems reasonable. Note how when we
have a sharp semblance maximum we see almost no variation, while
when our blob is more spread out, the selected gamma values are
more diverse. Note the fourth from the left gather at
1.8 seconds. Two different maxima are present in the semblance
gather and we see that both are picked by various realizations.
Figure 6 shows nine gamma maps as a function
of space. The 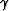 values are white when
values are white when 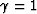 and
become more red has
and
become more red has 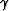 becomes lower, and more blue
as
becomes lower, and more blue
as 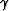 increases.
Note how we see a spatial consistency within a panel
but differences between the panels. The top-right portion
of the various realizations is especially interesting.
We see
increases.
Note how we see a spatial consistency within a panel
but differences between the panels. The top-right portion
of the various realizations is especially interesting.
We see 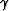 values greater than one, less than
one, and some mix of both are selected by the various realizations.
values greater than one, less than
one, and some mix of both are selected by the various realizations.
picks
Figure 4 Five different SM semblance scans at the
CRP locations shown in Figure 4. Overlaying the
semblance scans are 30 different 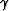 realizations.
Note the fourth from the left gather at
1.8 seconds. Two different maxims are present in the semblance
gather and we see that both are picked by various realizations.
realizations.
Note the fourth from the left gather at
1.8 seconds. Two different maxims are present in the semblance
gather and we see that both are picked by various realizations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 rand
rand
Figure 5 Nine realizations of random
numbers colored by applying fitting goals (12). Note
how the random numbers follow geologic dip but vary significantly
from image to image.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
 gamma_mult
gamma_mult
Figure 6 Nine realizations
of 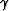 values using the random numbers shown in Figure 5.
Note how we see a spatial consistency within a panel
but differences between the panels.
values using the random numbers shown in Figure 5.
Note how we see a spatial consistency within a panel
but differences between the panels.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

The 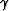 value were then used to update the
velocity model using a preconditioned version
of fitting goals (7). At this stage
we are so far away from the correct answer that
I limited the tomography to selecting back
projection shallower than 1.7 km. Figure 7
shows the selected back projection points overlaid
upon the migrated model.
Figure 8 shows nine realizations
of the tomography problem using the
value were then used to update the
velocity model using a preconditioned version
of fitting goals (7). At this stage
we are so far away from the correct answer that
I limited the tomography to selecting back
projection shallower than 1.7 km. Figure 7
shows the selected back projection points overlaid
upon the migrated model.
Figure 8 shows nine realizations
of the tomography problem using the 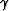 values shown
in Figure 6.
Note the variance in the velocity structure from
realization to realization. It is especially noticeable at
the fault through the anticline and to the left the
fault. We see velocity variations of 1 km/s or greater
between the various realizations. This isn't surprising given
the variance present in our semblance scans (Figure 4).
values shown
in Figure 6.
Note the variance in the velocity structure from
realization to realization. It is especially noticeable at
the fault through the anticline and to the left the
fault. We see velocity variations of 1 km/s or greater
between the various realizations. This isn't surprising given
the variance present in our semblance scans (Figure 4).
points
Figure 7 The points used to update the
velocity model using ray-based tomography overlaying
the initial migrated image.
|
|  |
 vel_mult
vel_mult
Figure 8 Nine realizations
of tomography using the 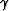 values shown in Figure 6.
Note the variation in the velocity structure especially to the left
of the fault cutting through the anticline.
values shown in Figure 6.
Note the variation in the velocity structure especially to the left
of the fault cutting through the anticline.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

As a final step, I migrated the data with the various velocity models.
Figure 9 shows the nine images corresponding
to the nine velocity models shown in Figure 8.
Note the differences in the various images. The top-right image
shows a much flatter basement reflector than any of the
other realizations. The variation in positioning of the fault reflector
is also significant between the various realizations.
image_mult
Figure 9 Nine realizations
corresponding
to the nine velocity models shown in Figure 8.
Note the differences in the various images. The top-right image
shows a much flatter basement reflector than any of the
other realizations. The variation positioning of the fault reflector
is also significant between the various realizations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)






Next: CONCLUSION
Up: R. Clapp: Velocity uncertainty
Previous: Limitations
Stanford Exploration Project
5/23/2004

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![]() ranging from
.7 to 1.3. Figure 4 shows the semblance
scans for the same five locations as in
Figure 3.
I used the initial migration image to construct a steering filter
for the colored random number generation.
Figure 5 shows nine realizations
of applying fitting goals (12). Note how the generated random
numbers follow the image structure shown in Figure 2, but
vary dramatically from realization to realization.
I converted these random numbers to
ranging from
.7 to 1.3. Figure 4 shows the semblance
scans for the same five locations as in
Figure 3.
I used the initial migration image to construct a steering filter
for the colored random number generation.
Figure 5 shows nine realizations
of applying fitting goals (12). Note how the generated random
numbers follow the image structure shown in Figure 2, but
vary dramatically from realization to realization.
I converted these random numbers to ![]() values using cdfs generated
at every location using equation (11). Thirty
realizations of
values using cdfs generated
at every location using equation (11). Thirty
realizations of ![]() values overlay the semblance scans
in Figure 4.
The various realizations are smooth as function of depth, which is reasonable.
The amount of variance also seems reasonable. Note how when we
have a sharp semblance maximum we see almost no variation, while
when our blob is more spread out, the selected gamma values are
more diverse. Note the fourth from the left gather at
1.8 seconds. Two different maxima are present in the semblance
gather and we see that both are picked by various realizations.
Figure 6 shows nine gamma maps as a function
of space. The
values overlay the semblance scans
in Figure 4.
The various realizations are smooth as function of depth, which is reasonable.
The amount of variance also seems reasonable. Note how when we
have a sharp semblance maximum we see almost no variation, while
when our blob is more spread out, the selected gamma values are
more diverse. Note the fourth from the left gather at
1.8 seconds. Two different maxima are present in the semblance
gather and we see that both are picked by various realizations.
Figure 6 shows nine gamma maps as a function
of space. The ![]() values are white when
values are white when ![]() and
become more red has
and
become more red has ![]() becomes lower, and more blue
as
becomes lower, and more blue
as ![]() increases.
Note how we see a spatial consistency within a panel
but differences between the panels. The top-right portion
of the various realizations is especially interesting.
We see
increases.
Note how we see a spatial consistency within a panel
but differences between the panels. The top-right portion
of the various realizations is especially interesting.
We see ![]() values greater than one, less than
one, and some mix of both are selected by the various realizations.
values greater than one, less than
one, and some mix of both are selected by the various realizations.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![]() value were then used to update the
velocity model using a preconditioned version
of fitting goals (7). At this stage
we are so far away from the correct answer that
I limited the tomography to selecting back
projection shallower than 1.7 km. Figure 7
shows the selected back projection points overlaid
upon the migrated model.
Figure 8 shows nine realizations
of the tomography problem using the
value were then used to update the
velocity model using a preconditioned version
of fitting goals (7). At this stage
we are so far away from the correct answer that
I limited the tomography to selecting back
projection shallower than 1.7 km. Figure 7
shows the selected back projection points overlaid
upon the migrated model.
Figure 8 shows nine realizations
of the tomography problem using the ![]() values shown
in Figure 6.
Note the variance in the velocity structure from
realization to realization. It is especially noticeable at
the fault through the anticline and to the left the
fault. We see velocity variations of 1 km/s or greater
between the various realizations. This isn't surprising given
the variance present in our semblance scans (Figure 4).
values shown
in Figure 6.
Note the variance in the velocity structure from
realization to realization. It is especially noticeable at
the fault through the anticline and to the left the
fault. We see velocity variations of 1 km/s or greater
between the various realizations. This isn't surprising given
the variance present in our semblance scans (Figure 4).


![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
