Next: PEFs in the data
Up: Curry: Regularizing Madagascar: PEFs
Previous: INTRODUCTION
The Madagascar regularization problem has been approached using the following fitting goals Lomask (2002):
| ![\begin{eqnarray}
\ {\bf W} \frac{d}{dt}[{\bf L}{\bf m} -{\bf d}] &\approx& {\bf 0} \nonumber \\ \ \epsilon {\bf A m} &\approx& {\bf 0} .
\end{eqnarray}](img1.gif) |
|
| (1) |
In these fitting goals: W corresponds to a weight for ends of tracks and spikes in the data, 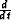 is a derivative along each track used to
eliminate low frequency variations along each track,
L is a linear interpolation operator that moves from values on a regular grid to the data points,
m is the desired gridded model, d are the data points along the tracks, A is a regularization operator, and
is a derivative along each track used to
eliminate low frequency variations along each track,
L is a linear interpolation operator that moves from values on a regular grid to the data points,
m is the desired gridded model, d are the data points along the tracks, A is a regularization operator, and  is a trade-off
parameter between the two fitting goals.
is a trade-off
parameter between the two fitting goals.
The regularization operator (A) typically is a Laplacian, a prediction-error filter (PEF), or a non-stationary PEF Crawley (2000). When using a PEF,
it first must be estimated on some training data, using a least-squares fitting goal,
| 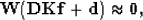 |
(2) |
in which W is a weight to exclude equations with missing data, D is convolution with the data, K constrains the
first filter coefficient to 1, f is the unknown filter, and d is a copy of the data.
In order to set a benchmark for how effective a prediction-error filter can be as a regularization operator,
a PEF is estimated on the densely-sampled portion of the Madagascar dataset and is then used to interpolate the sparse
tracks in the same area. The data are interpolated by using the following fitting goals:
| 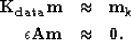 |
|
| (3) |
Here 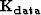 is a mask for known data,
is a mask for known data, 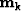 are the data,
are the data, 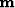 is the model, and
A is the regularization operator. In this case, the input data is the output of the fitting
goals in equation (1), with
is the model, and
A is the regularization operator. In this case, the input data is the output of the fitting
goals in equation (1), with  set to zero. Results for using a Laplacian, a PEF estimated
on well-sampled data, and a non-stationary PEF estimated on dense data as the regularization operator
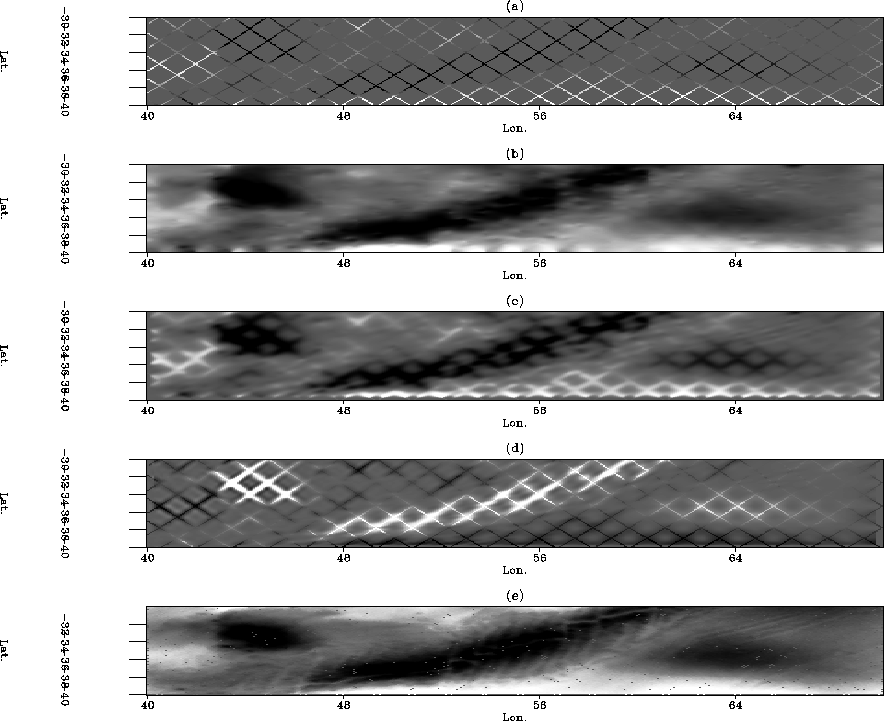
A are all shown in Figure 1. As we can see, as the complexity of the regularization operator
increases, the interpolated result improves. This is because the Laplacian assumes isotropic behavior in the data
while the PEF and non-stationary PEF are based on statistical information in the data. The PEF assumes statisical
stationarity in the data while the non-stationary recognizies and accounts for the non-stationary nature of the data.
These results set an upper benchmark for what the best possible interpolation could be using these methods for this type
of dataset. In this example we are benefiting from the fully sampled nature of the input.
sparsedata
set to zero. Results for using a Laplacian, a PEF estimated
on well-sampled data, and a non-stationary PEF estimated on dense data as the regularization operator
A are all shown in Figure 1. As we can see, as the complexity of the regularization operator
increases, the interpolated result improves. This is because the Laplacian assumes isotropic behavior in the data
while the PEF and non-stationary PEF are based on statistical information in the data. The PEF assumes statisical
stationarity in the data while the non-stationary recognizies and accounts for the non-stationary nature of the data.
These results set an upper benchmark for what the best possible interpolation could be using these methods for this type
of dataset. In this example we are benefiting from the fully sampled nature of the input.
sparsedata
Figure 1 When we know the answer, from top to bottom: (a) The sparse tracks on the lower half of the data set;
(b) Those tracks interpolated with Laplacian regularization; (c) The sparse tracks interpolated with a PEF estimated on the co-located dense tracks;
(d) the same as (c), but using a non-stationary PEF; (e) the dense tracks from the same area.

Now that the best-case scenarios are out of the way, we can see what we can accomplish without
cheating and using the dense data. By using only the sparse tracks, we are not able to capture nearly
as much information about the model as we have in the previous case. The results for interpolating with a Laplacian
as well as stationary and non-stationary PEFs estimated solely on the sparse tracks with the multi-scale method
Curry and Brown (2001); Curry (2002, 2003) are shown in Figure 2.
unrotpef
Figure 2 When we don't know the answer, from top to bottom:(a) The sparse tracks on the lower half of the data set;
(b) Those tracks interpolated with Laplacian regularization; (c) The sparse tracks interpolated with a PEF estimated on the same sparse tracks;
(d) the same as (c), but using a non-stationary PEF; (e) the dense tracks from the same area.

In this case, there are regions of the data where the Laplacian gives the best result, and regions where the non-stationary PEF gives the best result.
One example of this is the spreading ridge. The non-stationary PEF is able to interpolate some fine features of the ridge that Laplacian interpolation is incapable of.
However, in other regions, the non-stationary PEF performs poorly, and the far simpler Laplacian interpolation gives a more reasonable result.
This is because the PEFs estimated using the multi-scale approach do not always properly characterize the data, as local information is destroyed in the
multi-scale averaging process.
Some of the problems encountered by the non-stationary PEF are due to the spatial distribution of the data. The multi-scale approach used in Figure 2
blindly rescales the data without regard to their location. By simply making the grid cells larger, very coarse bins must be used before
the data become contiguous, and many data points along the tracks fall into these bins. We are clearly in need of a
method that will take into account that these data are collected along curved tracks that are at an angle.





Next: PEFs in the data
Up: Curry: Regularizing Madagascar: PEFs
Previous: INTRODUCTION
Stanford Exploration Project
5/23/2004
![\begin{eqnarray}
\ {\bf W} \frac{d}{dt}[{\bf L}{\bf m} -{\bf d}] &\approx& {\bf 0} \nonumber \\ \ \epsilon {\bf A m} &\approx& {\bf 0} .
\end{eqnarray}](img1.gif)
![\begin{eqnarray}
\ {\bf W} \frac{d}{dt}[{\bf L}{\bf m} -{\bf d}] &\approx& {\bf 0} \nonumber \\ \ \epsilon {\bf A m} &\approx& {\bf 0} .
\end{eqnarray}](img1.gif)