




Next: A Gulf of Mexico
Up: Guitton et al.: Velocity
Previous: Estimation of time shifts
From the time shifts, we
estimate interval velocities in the  domain. As pointed out
by Alkhalifah (2003) and Clapp (2001),
domain. As pointed out
by Alkhalifah (2003) and Clapp (2001),
 tomography is more robust than depth tomography to reflector position and velocity
errors. However, going from depth to vertical travel time
introduces new variables. As described by
Biondi et al. (1997) and Alkhalifah (2003), the
transformation from depth coordinates (x,z) into
vertical-traveltime coordinates
tomography is more robust than depth tomography to reflector position and velocity
errors. However, going from depth to vertical travel time
introduces new variables. As described by
Biondi et al. (1997) and Alkhalifah (2003), the
transformation from depth coordinates (x,z) into
vertical-traveltime coordinates 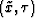 is governed by the
relationships:
is governed by the
relationships:
| 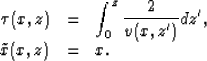 |
(7) |
Therefore, we have the following relationships between the
differential quantities (dx,dz) and 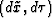 :
:
| 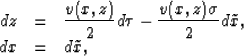 |
(8) |
where v(x,z) is the focusing velocity proportional to the mapping
velocity Clapp (2001) and
| 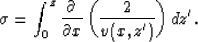 |
(9) |
In this paper, it is assumed that 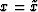 and
and 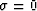 because the initial slowness field is horizontally
invariant.
because the initial slowness field is horizontally
invariant.
The data space for this inverse problem is a cube of
time-shifts at every time, offset and midpoint location. This
differs from most tomographic techniques where
a few reflectors are usually selected and picked for the inversion.
The number of the model space unknowns (the velocity update) is
the product of the number of gathers and the number of time samples.
A velocity perturbation is computed for each pixel in the model space.
For a CMP location x at time  and offset h, a total
time shift ts is estimated. The forward problem relating
velocity perturbation and time shift is derived from
Fermat's principle:
and offset h, a total
time shift ts is estimated. The forward problem relating
velocity perturbation and time shift is derived from
Fermat's principle:
| 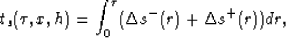 |
(10) |
with
| 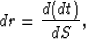 |
(11) |
where 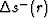 and
and 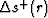 are the slowness
perturbations along the down- and up-going rays respectively (from
x-h/2 to x and x+h/2 to x),
S is the focusing slowness, and dt the time increment along the
ray Clapp and Biondi (2000). Note that slownesses are
actually estimated and not velocities, as it is usually done in tomography.
To simplify the problem, we assume that the up- and
down-going rays are straight lines in the
are the slowness
perturbations along the down- and up-going rays respectively (from
x-h/2 to x and x+h/2 to x),
S is the focusing slowness, and dt the time increment along the
ray Clapp and Biondi (2000). Note that slownesses are
actually estimated and not velocities, as it is usually done in tomography.
To simplify the problem, we assume that the up- and
down-going rays are straight lines in the 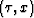 space.
space.
Equation (10) is
a linear relationship between the time shifts and the
slowness perturbations allowing us to write,
| 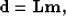 |
(12) |
where 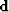 are the estimated time shifts,
are the estimated time shifts, 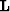 is the tomographic operator in equation (10) and
is the tomographic operator in equation (10) and
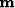 is a field of slowness perturbations. Our goal is to find
is a field of slowness perturbations. Our goal is to find
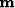 such that,
such that,
| 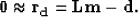 |
(13) |
The addition of a regularization operator to enforce smoothness in the
horizontal direction gives:
| 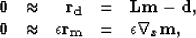 |
(14) |
where 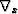 is the horizontal gradient.
Next,
is the horizontal gradient.
Next, 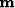 is estimated in a least-squares sense by minimizing
objective function,
is estimated in a least-squares sense by minimizing
objective function,
| 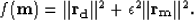 |
(15) |
In practice, 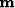 is estimated with a conjugate-gradient method
and
is estimated with a conjugate-gradient method
and  is estimated by trial and error. Because
tomography is inherently non-linear,
more iterations are needed to converge
toward a satisfying velocity model.
However, the assumptions made in this paper do not allow us to iterate without
using more sophisticated imaging operators or ray tracing
tools. We now test our method on a 2D Gulf of Mexico dataset.
is estimated by trial and error. Because
tomography is inherently non-linear,
more iterations are needed to converge
toward a satisfying velocity model.
However, the assumptions made in this paper do not allow us to iterate without
using more sophisticated imaging operators or ray tracing
tools. We now test our method on a 2D Gulf of Mexico dataset.





Next: A Gulf of Mexico
Up: Guitton et al.: Velocity
Previous: Estimation of time shifts
Stanford Exploration Project
5/23/2004
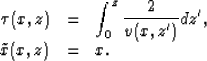
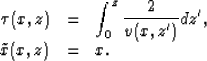
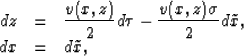
![]() and offset h, a total
time shift ts is estimated. The forward problem relating
velocity perturbation and time shift is derived from
Fermat's principle:
and offset h, a total
time shift ts is estimated. The forward problem relating
velocity perturbation and time shift is derived from
Fermat's principle: