Signal/noise separation results

The goal of this section is to compare the two subtraction techniques on the synthetic dataset. This dataset was primarily designed to conduct blind tests for velocity estimation methods. Consequently, no structural information is known.

The result of adaptive subtraction is shown for one offset section in Figure 3 and the result of pattern-based subtraction is shown in Figure 4. The adaptive subtraction is doing a decent job everywhere. However, some multiples are still visible. For example, '1' in Figure 3 points to a location where multiples overlap with primaries and are not attenuated. In contrast, the pattern-based subtraction technique (i.e., Figure 4) seems to do a better job attenuating these events. The same is true for arrows '2' and '5'. The diffracted multiples (arrows '3' and '4') are also better attenuated with the pattern-based technique.

 

dsign
Figure 3 Constant offset section (h=550 m) of the estimated primaries with adaptive subtraction. The arrows point to locations where multiples are still present.

 

sign
Figure 4 constant offset section (h=550 m) of the estimated primaries with pattern recognition. Multiples are better attenuated than in Figure 3.

Because no velocity analysis was conducted with this dataset, no stacks are presented. Alternatively, close-ups of constant offset sections are shown to illustrate strengths and weaknesses of the two different approaches. Figure 5 shows a comparison between the input data, the multiple model, the estimated primaries with the adaptive subtraction and the estimated primaries with the pattern recognition technique. The offset is 700 m. As shown by the arrows, the pattern-based method performs generally better. The same conclusions hold in Figure 6. Note in Figure 6b aliasing artifacts due to the coarse sampling of the offset axis for the multiple prediction van Dedem (2002).

Sometimes, it can be rather difficult to see if multiples are removed or not by simply looking at 2D planes. Figure 7c shows one event at '2' that seems to be a primary. However, by looking at the shot gathers (not shown here), it appears that this event is a multiple that the pattern-based approach was able to attenuate.

One shortcoming of the pattern-recognition technique is that it relies on the Spitz approximation to provide a signal model if nothing else is available. By construction, the signal and noise filters will span different components of the dataspace. Therefore, the estimated primaries and multiples are uncorrelated. This simple fact proves that with the Spitz approximation, higher dimension filters are preferred because primaries and multiples have fewer chances to look similar.

Figure 8 shows an example where primaries are damaged by the pattern-based method. For instance in Figure 8a, we see at '2' a primary that is attenuated by the PEFs (Figure 8d) but well preserved by the adaptive subtraction (Figure 8c). Here the primaries and multiples (Figure 8b) exhibit similar patterns. Using the Spitz approximation, event '2' is identified as noise and removed as such. For event '3', it is quite difficult to say if multiples are better removed in Figure 8d or if primaries are better preserved in Figure 8c. Looking at the corresponding shot gathers did not help to make a decision because the multiples are very strong. Event '4' looks clearly better with the adaptive subtraction and '1' and '5' are well recovered with the pattern-based approach.

 

compwin1
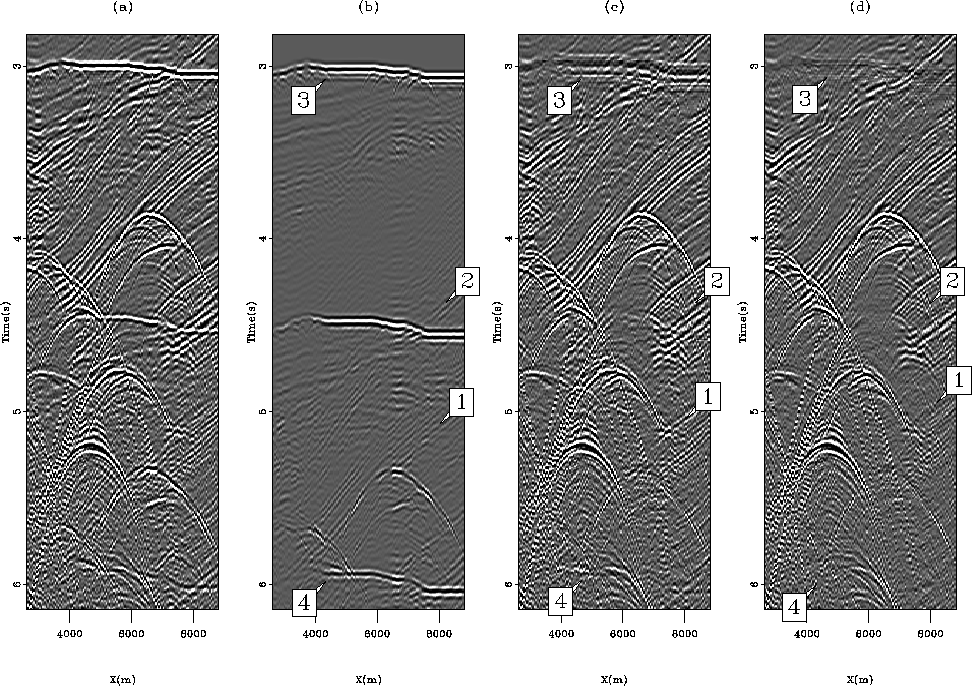
Figure 5 Constant offset sections (h=700 m) for (a) the input data, (b) the multiple model, (c) the estimated primaries with adaptive subtraction and (d), estimated primaries with the pattern-based approach. Arrows point to locations where the pattern-based approach attenuates multiples significantly better than the adaptive subtraction.

 

compwin6
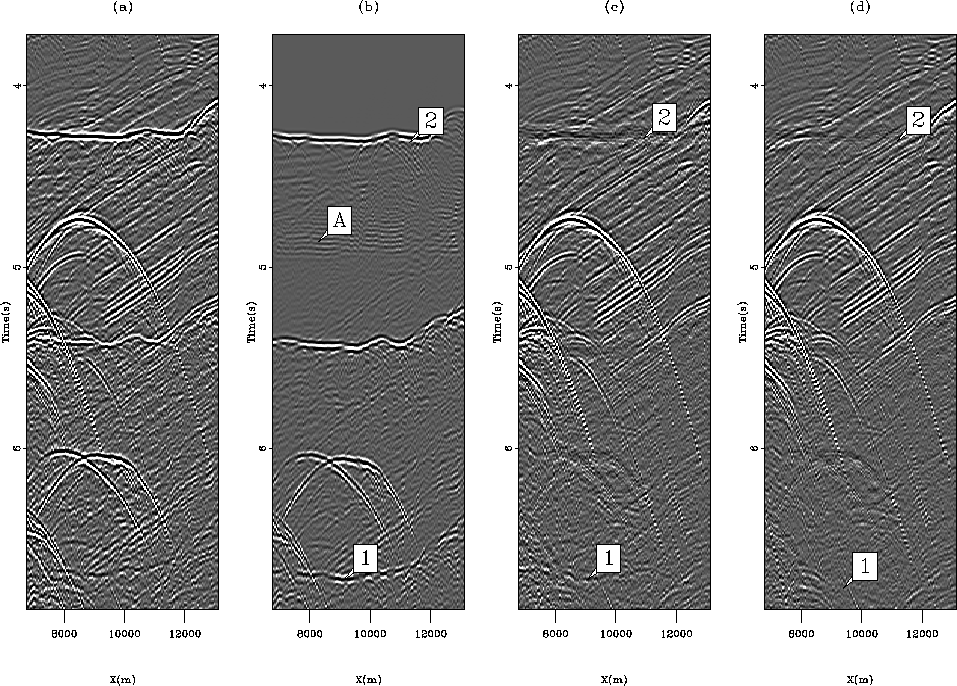
Figure 6 Constant offset sections (h=4550 m) for (a) the input data, (b) the multiple model, (c) the estimated primaries with adaptive subtraction and (d), estimated primaries with the pattern-based approach. Arrow A points to aliasing effects due to the offset sampling of the shot gathers. The pattern-based approach attenuates the multiples better than the adaptive subtraction in '1' and '2'.

 

compwin8
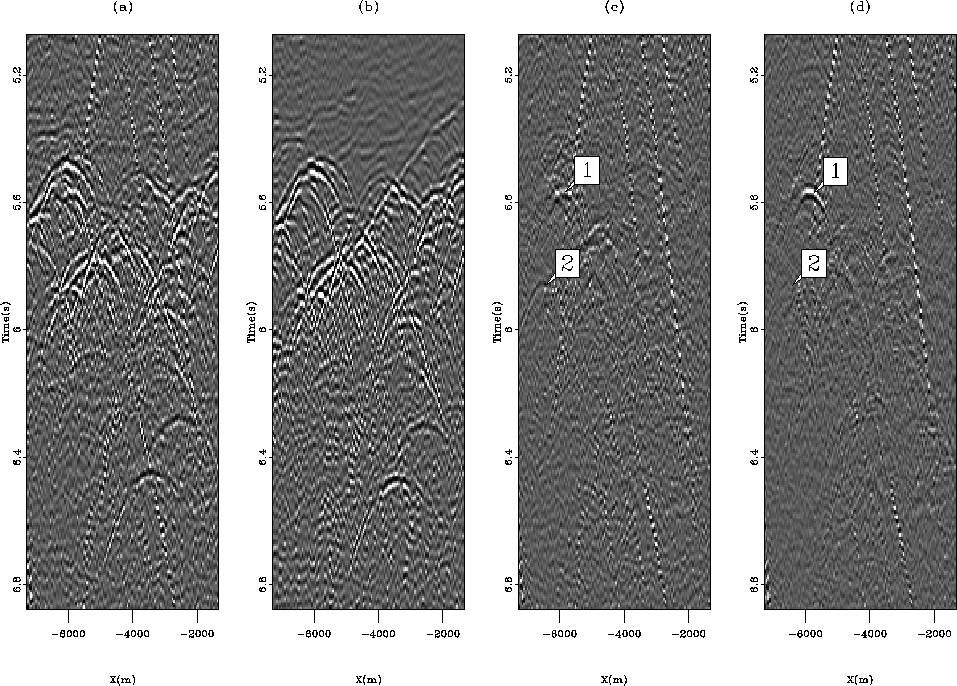
Figure 7 Constant offset sections (h=3300 m) for (a) the input data, (b) the multiple model, (c) the estimated primaries with adaptive subtraction and (d), estimated primaries with the pattern-based approach. '1' points to a primary that the pattern-recognition preserves very well. '2' points to an event that is attenuated with the pattern-based approach but not with the adaptive subtraction in (c). Though not shown here, a close inspection of the corresponding shot gathers suggests that '2' is actually a multiple.

 

compwin12
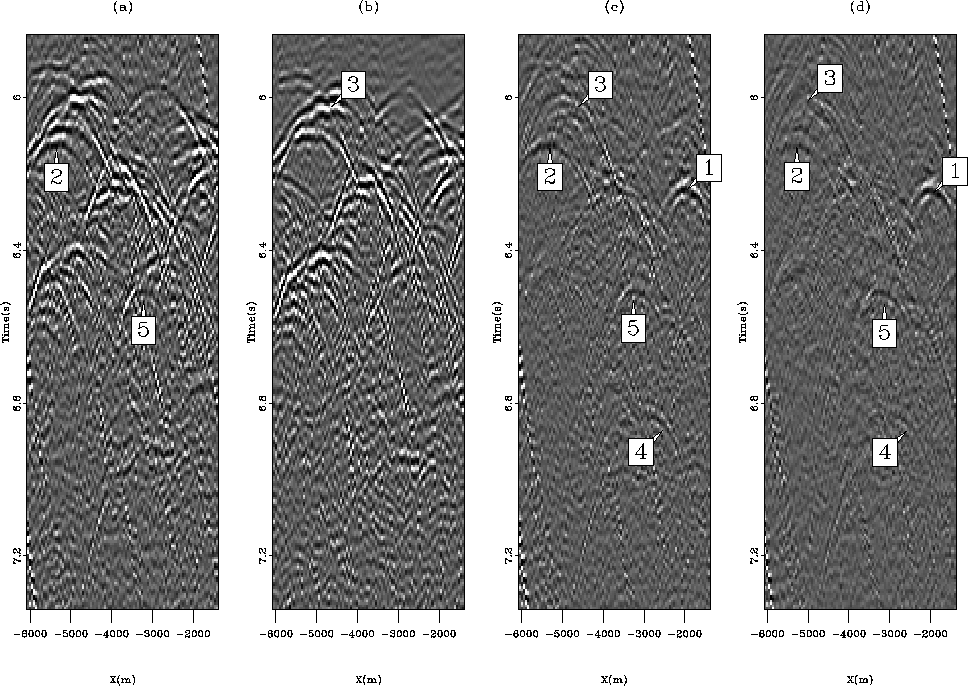
Figure 8 Constant offset sections (h=5050 m) for (a) the input data, (b) the multiple model, (c) the estimated primaries with adaptive subtraction and (d), estimated primaries with the pattern-based approach. '1' and '5' show events better preserved with the pattern-based method. '2' and '1' are better recovered with the adaptive subtraction. '4' seems to point to a primary that the adaptive subtraction is able to save. '3' is undecided.