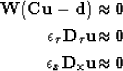Dix equation as a Least-Squares problem

The Dix Equation states the nonlinear relationship between RMS velocity and interval velocity. Harlan (1999) linearizes the relationship and solves the problem using a Gauss-Newton nonlinear iteration. However, the problem is linear in the square of the interval velocity. This ``linear'' problem was solved by Clapp et al. (1998). They apply a preconditioned least squares optimization to ``invert'' Dix equation, with spatial smoothness constraints.

Let us rewrite for completeness the Dix equation as a least-squares fitting goal:  

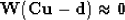$$\bf W ( Cu - d ) \approx 0$$ (1)

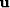where $\bf u$ is the unknown model, a vector of squared interval velocities. 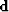$\bf d$ is the known data, a vector of squared RMS velocities multiplied by time. 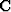$\bf C$ is the causal integration operator. 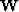$\bf W$ is a data residual weighting function, which is proportional to our confidence in the RMS velocities.

Fitting goal (1) is notoriously unstable to high frequency variations in RMS velocity, and moreover, it is under-determined in the sense that only strong reflections really qualify as ``data''. Therefore, Clapp et al. (1998) supplement the system with a regularization term which penalizes ``wiggliness''. In our case we use first order derivatives, but as we will see later, other rougheners can be used:

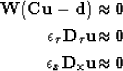$$\begin{eqnarray} \bf W ( Cu - d ) \approx 0 \\ \epsilon_{\tau} { \bf D_{\tau} u} { \bf \approx 0 } \\ \epsilon_{x} { \bf D_x u} { \bf \approx 0 }\end{eqnarray}$$ (2) (3) (4)

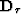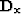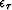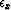where ${ \bf D_{\tau} }$ and ${ \bf D_x }$ are first-order finite differences derivatives in time and midpoint, respectively, and the scalars $\epsilon_{\tau}$ and $\epsilon_{x}$ balance the relative importance of the two model residuals.

In hard rock environments like carbonates, velocities tend to be homogeneous for intervals, with abrupt discontinuities at changes in lithology. There, the desire for a blocky interval velocity model is well-justified.