| |
(1) |
| |
(2) |
From Equations (1) and (2), we can write that
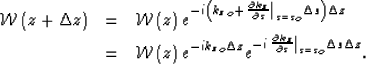 |
(3) | |
| (4) |
Equation (3) represents a general form of the main mixed-domain downward-continuation operator. This operator can be broken up into a group of functional operators as follows:
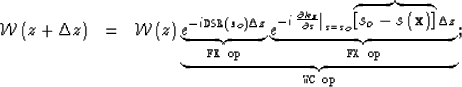 |
(5) |
| |
(6) |
For Equations (5) and (6), we can distinguish 5 functional operators. Each operator is initialized with a call to a function (XXin) and executed with a call to another function (XXop). In a typical example, the functional operators perform the following tasks:
Continues the wavefield between two depth levels, using one or more reference slownesses.
Interface: integer function WCop(wfld,iws,izs,ith,FKop,FXop) result(st)
Implemented examples:
Selects the number and values of the reference slownesses (so), and sets-up the interpolation map between the wavefields continued using the various reference slownesses.
Interface: integer function SLop() result(st)
Implemented examples:
Performs phase-shift using the full 3-D DSR equation Claerbout (1985), the common-azimuth equation Biondi and Palacharla (1996), or the offset plane-waves equation Mosher and Foster (2000).
Interface: integer function FXop(iws,izs,ifk,ith,wfld) result(st)
Implemented examples:
Performs phase shift that accounts for lateral slowness variation. Examples of (f-x) operators include but are not limited to split-step Fourier Stoffa et al. (1990), local Born Fourier or local Rytov Fourier Huang et al. (1999), Fourier Finite-Difference Ristow and Ruhl (1994), generalized screen propagators Le Rousseau and de Hoop (1998), etc.
Interface: integer function FXop(iws,izs,ifk,ith,wfld) result(st)
Implemented example:
Performs imaging in the offset-domain or the offset ray-parameter domain. This operator can also incorporate amplitude-preserving corrections.
Interface: integer function IGop(wfld,iws,ith) result(st)
Implemented examples: